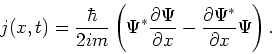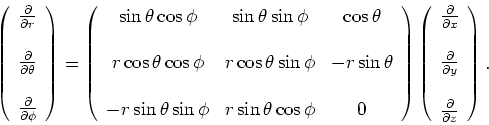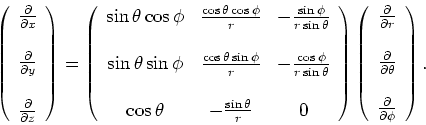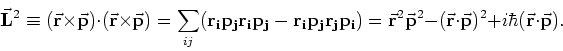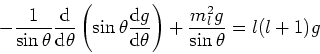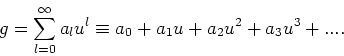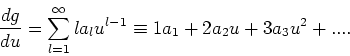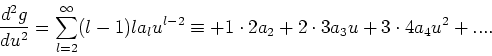- ... licht1
- We gebruiken deze term in
algemene zin om niet alleen het zichtbare licht, maar
het gehele elektromagnetische spectrum aan te duiden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
produkt2
- In het algemeen kunnen toestandfuncties complex zijn.
We definiëren het scalaire produkt in dat geval
als
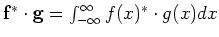 .
Men schrijft dit ook wel als
.
Men schrijft dit ook wel als
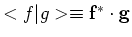 ,
waarbij de `bra'
,
waarbij de `bra' 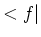 de complex geconjugeerde is van de `ket'
de complex geconjugeerde is van de `ket'
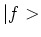 . Deze laatste notatie is ingevoerd door Dirac. Merk op
dat geldt
. Deze laatste notatie is ingevoerd door Dirac. Merk op
dat geldt
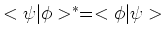 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... eigenwaarden3
- In het Dirac formalisme is een
operator
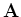 hermitisch als voor elke twee kets
hermitisch als voor elke twee kets 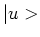 en
en
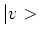 geldt dat
geldt dat
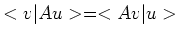 . We kunnen dit
schrijven als
. We kunnen dit
schrijven als
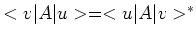 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
waarschijnlijkheid4
- Merk op dat in het geval van een complexe
toestandsfunctie deze waarschijnlijkheid gegeven wordt door
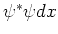 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... plaats5
- Merk
op dat men meestal de operator
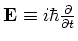 aantreft, die van onze definitie
verschilt in een minteken. Later in dit college zal uitgelegd worden
waar deze keuzemogelijkheid vandaan komt.
aantreft, die van onze definitie
verschilt in een minteken. Later in dit college zal uitgelegd worden
waar deze keuzemogelijkheid vandaan komt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... deel6
- Merk op dat
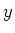 een
reëel getal is.
een
reëel getal is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
aangetroffen7
- Als we de notatie
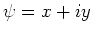 gebruiken,
dan volgt direct dat
gebruiken,
dan volgt direct dat
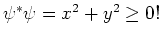 en zien we dat
deze kans altijd reëel en positief is.
en zien we dat
deze kans altijd reëel en positief is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... werkt8
- De kracht wordt gegeven door
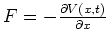 en voor een constante potentiaal
werkt er geen kracht op het deeltje.
en voor een constante potentiaal
werkt er geen kracht op het deeltje.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... oplossing9
- Een tweede-orde differentiaalvergelijking van
het type
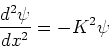 |
(122) |
heeft voor 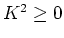 als meest algemene oplossing de functie
als meest algemene oplossing de functie
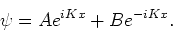 |
(123) |
Hierbij zijn 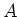 en
en 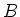 constanten.
constanten.
Als geldt dat 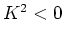 , dan kan de meest algemene oplossing geschreven
worden als
, dan kan de meest algemene oplossing geschreven
worden als
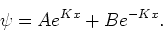 |
(124) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... oplossing10
- Merk op dat vanwege
 we nu te maken hebben met geval
we nu te maken hebben met geval 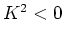 ! Zie ook de opmerkingen in
voetnoot 4.
! Zie ook de opmerkingen in
voetnoot 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... oplossing11
- Merk op dat vanwege
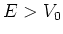 we nu te maken hebben met geval
we nu te maken hebben met geval 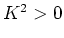 ! Zie ook de opmerkingen in
voetnoot 4.
! Zie ook de opmerkingen in
voetnoot 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... waarschijnlijkheidsflux12
- We interpreteren
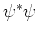 als waarschijnlijkheidsdichtheid. Met deze interpretatie
kunnen we een nieuwe locale grootheid invoeren die de stroming (flux)
van de waarschijnlijkheid aangeeft. We beschouwen eerst de vergelijkingen
voor vrije deeltjes die beschreven worden door de golffuncties
als waarschijnlijkheidsdichtheid. Met deze interpretatie
kunnen we een nieuwe locale grootheid invoeren die de stroming (flux)
van de waarschijnlijkheid aangeeft. We beschouwen eerst de vergelijkingen
voor vrije deeltjes die beschreven worden door de golffuncties 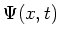 en
en 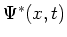 . Er geldt
. Er geldt
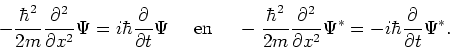 |
(151) |
Merk op dat beide vergelijkingen gerelateerd zijn door complexe
conjugatie. We gebruiken deze uitdrukkingen om de tijdsafhankelijkheid
van de waarschijnlijkheidsdichtheid van een vrij deeltje te analyseren.
![\begin{displaymath}
\begin{array}{rl}
{\partial \over \partial t} \left( \Psi^* ...
...\Psi^* \over \partial x} \Psi \right) \right] . \\
\end{array}\end{displaymath}](img422.gif) |
(152) |
Deze vergelijking kan herschreven worden tot
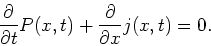 |
(153) |
Bovenstaande vergelijking drukt het behoud van waarschijnlijkheid
in de tijd uit. Elke verandering in de tijd van de waarschijnlijkheidsdichtheid
in een locaal gebied wordt gecompenseerd door een flux van waarschijnlijkheid
in of uit dat locale gebied. Hiermee wordt ook de
waarschijnlijkheidsflux geïntroduceerd, waarvoor geldt
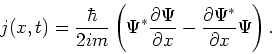 |
(154) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... worden13
- Een
elegante manier om deze uitdrukkingen af te leiden, is door gebruik
van matrixnotatie. Er geldt
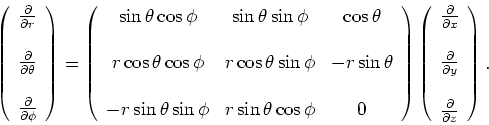 |
(200) |
We kunnen deze matrix inverteren en verkrijgen op deze wijze uitdrukkingen
voor de operatoren
 ,
,
 en
en
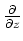 . Er geldt
. Er geldt
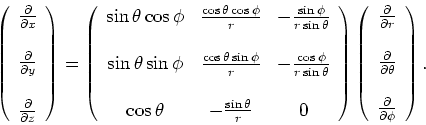 |
(201) |
We kunnen de juistheid van bovenstaande uitdrukking controleren
door de twee matrices te vermenigvuldigen, waarbij het resultaat
de eenheidsmatrix dient te zijn. Vervolgens is het mogelijk de
componenten van 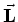 te berekenen. Bijvoorbeeld hebben
we
te berekenen. Bijvoorbeeld hebben
we
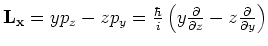 , waarbij we de geïnverteerde
matrix gebruiken als we de afgeleiden invullen.
, waarbij we de geïnverteerde
matrix gebruiken als we de afgeleiden invullen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vectoren14
- Als we deze stelling
toepassen op operatoren, dan dienen we rekening te houden met
de volgorde van de operatoren. Dit omdat de componenten van de operatoren
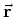 en
en 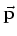 niet commuteren. Er geldt
niet commuteren. Er geldt
![$[ r_i , p_j ]=r_ip_j - p_jr_i = i\hbar \delta_{ij}$](img519.gif) .
.
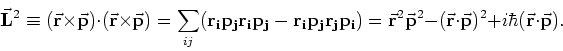 |
(204) |
We gebruiken verder de relatie
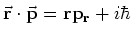 en vinden hiermee het gewenste resultaat.
en vinden hiermee het gewenste resultaat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
oplossen15
- De differentiaalvergelijking
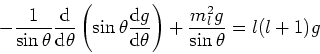 |
(232) |
kan worden opgelost door aan te nemen dat de oplossing
geschreven kan worden als een machtreeks,
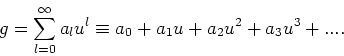 |
(233) |
Er geldt dan voor de eerste afgeleide
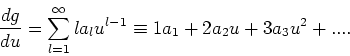 |
(234) |
en voor de tweede afgeleide
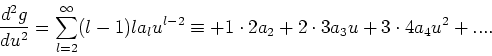 |
(235) |
We substitueren deze uitdrukkingen in de differentiaalvergelijking en
stellen de eis dat de individuele coëfficienten voor elke macht
van 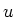 gelijk aan nul dienen te zijn. Dit levert een recursierelatie
en de algemene oplossing, waarbij
gelijk aan nul dienen te zijn. Dit levert een recursierelatie
en de algemene oplossing, waarbij
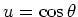 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (gereduceerde16
- De
gereduceerde massa voor een twee-deeltjessysteem is gegeven door
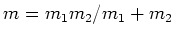 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() , dan kan de meest algemene oplossing geschreven
worden als
, dan kan de meest algemene oplossing geschreven
worden als
![\begin{displaymath}
\begin{array}{rl}
{\partial \over \partial t} \left( \Psi^* ...
...\Psi^* \over \partial x} \Psi \right) \right] . \\
\end{array}\end{displaymath}](img422.gif)