


Next: Matrices en Operatoren
Up: Wiskundig Intermezzo
Previous: Wiskundig Intermezzo
Er zijn vele manieren om quantummechanica te leren: historisch,
empirisch, Hamiltonisch, axiomatisch enz. We kiezen hier de
axiomatische wijze omdat die het snelst tot een nivo leidt
waarbij we de belangrijkste elementaire problemen te lijf kunnen gaan.
De grootste hindernis is het overwinnen van de abstracte en
ongewone taal. We zullen hier beginnen met de benodigde wiskundige achtergrond.
David Hilbert heeft ingezien dat functies zich formeel net
zo gedragen als vectoren. Dit kan men logisch aannemelijk maken
door te bewijzen dat functies voldoen aan dezelfde
axiomas als vectoren, waaruit dan alle eigenschappen van de vectorruimte volgen.
De functies bouwen ook een dergelijke ruimte op, die de Hilbertruimte
genoemd wordt.
Na al deze overeenstemmingen willen we op het wezenlijke verschil tussen
een vector en een functie wijzen: een functie is een vector met
oneindig veel dimensies. Hierdoor hebben twee functies veel meer mogelijkheden
om niet parallel te zijn in vergelijking met twee vectoren. Functies
hebben bijvoorbeeld meer mogelijkheden orthogonaal te zijn.



Next: Matrices en Operatoren
Up: Wiskundig Intermezzo
Previous: Wiskundig Intermezzo
Jo van den Brand
2000-10-21
![]() wordt gedefinieerd door aan elke
waarde van het argument
wordt gedefinieerd door aan elke
waarde van het argument ![]() (meestal met
(meestal met
![]() )
een getal toe te voegen, dat de functiewaarde
)
een getal toe te voegen, dat de functiewaarde ![]() voorstelt.
voorstelt.![]() en
en ![]() kunnen worden opgeteld tot
een nieuwe functie
kunnen worden opgeteld tot
een nieuwe functie ![]() , indien men voor elk argument
, indien men voor elk argument ![]() de
functiewaarde
de
functiewaarde ![]() en
en ![]() optelt en de som gelijk stelt aan
optelt en de som gelijk stelt aan ![]() .
.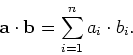
![]() en
en ![]() wordt verkregen door voor elk argument
wordt verkregen door voor elk argument ![]() de functiewaarden
te vermenigvuldigen. De integraal van al deze produkten wordt het scalaire
produkt2 genoemd,
de functiewaarden
te vermenigvuldigen. De integraal van al deze produkten wordt het scalaire
produkt2 genoemd,
