We beschouwen de beweging van een elektron met (gereduceerde16) massa
![]() onder invloed van de Coulomb potentiaal
onder invloed van de Coulomb potentiaal
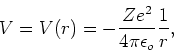 |
(251) |
![\begin{displaymath}
\left[ -{\hbar^2 \over 2m}\Delta_r -{Ze^2 \over 4\pi\epsilon_0r} \right]
\psi (\vec r) =E\psi (\vec r) .
\end{displaymath}](img623.gif) |
(252) |
Vervolgens definiëren we de dimensieloze variabelen
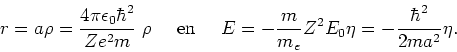 |
(254) |
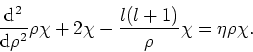 |
(255) |
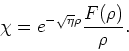 |
(256) |
|
|
waarbij dient te gelden dat ![]() .
Bovenstaande differentiaalvergelijking kan weer opgelost worden
door aan te nemen dat de oplossing als een machtreeks kan worden
geschreven. We vinden dan als oplossing
.
Bovenstaande differentiaalvergelijking kan weer opgelost worden
door aan te nemen dat de oplossing als een machtreeks kan worden
geschreven. We vinden dan als oplossing
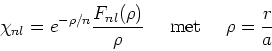 |
(257) |
We noemen de integer ![]() het hoofdquantumgetal, waarbij
het hoofdquantumgetal, waarbij ![]() de energie van de toestand bepaald
de energie van de toestand bepaald
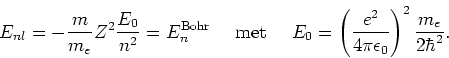 |
(258) |
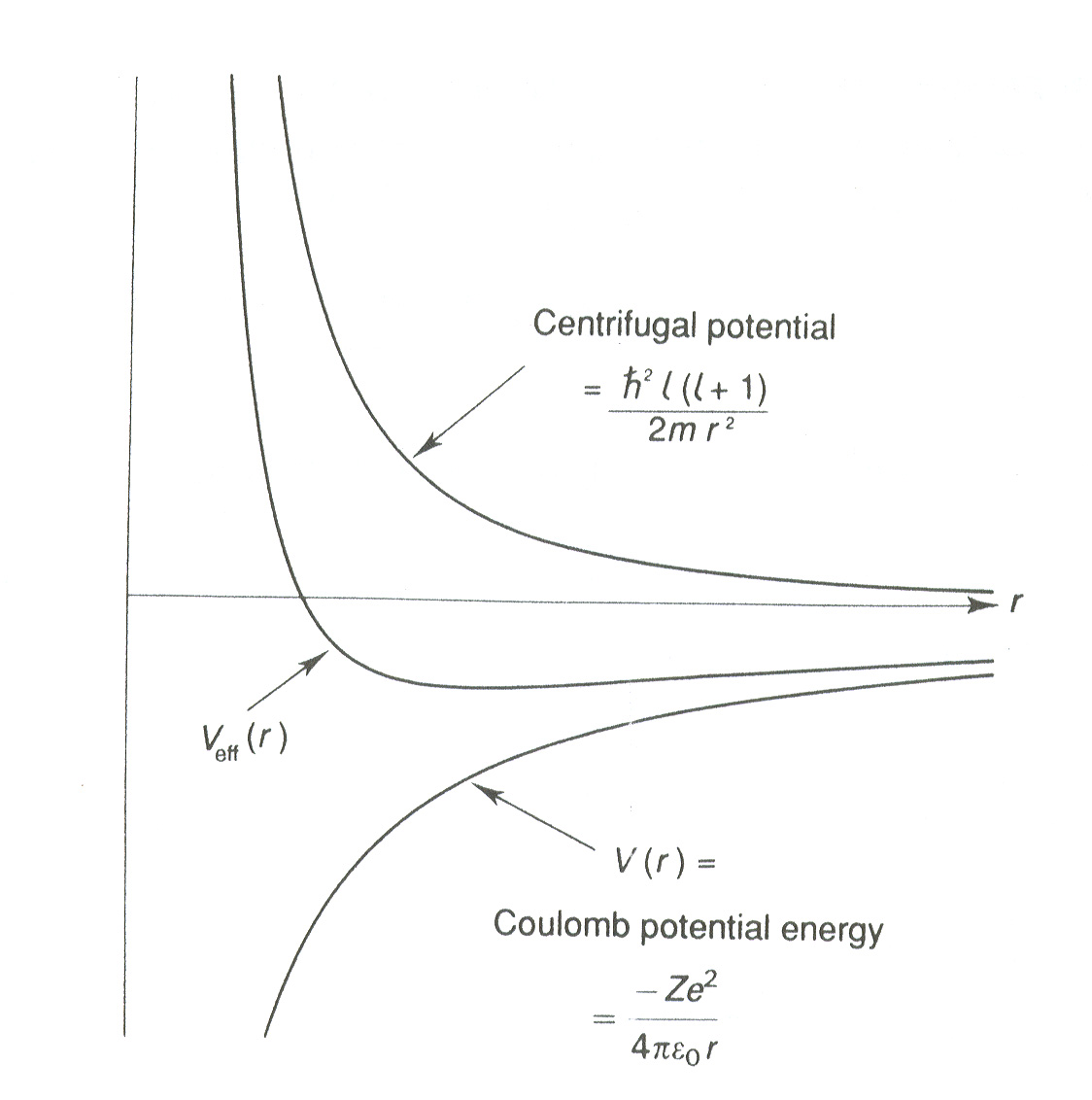
We constateren dat voor de Coulomb potentiaal, net als voor elke andere
potentiaal die tot gebonden toestanden leidt, de toegestane energieën
van een deeltje dat zich beweegt in deze potentiaal discreet
gequantiseerd is. De energieniveaus worden getoond in Fig. 27.
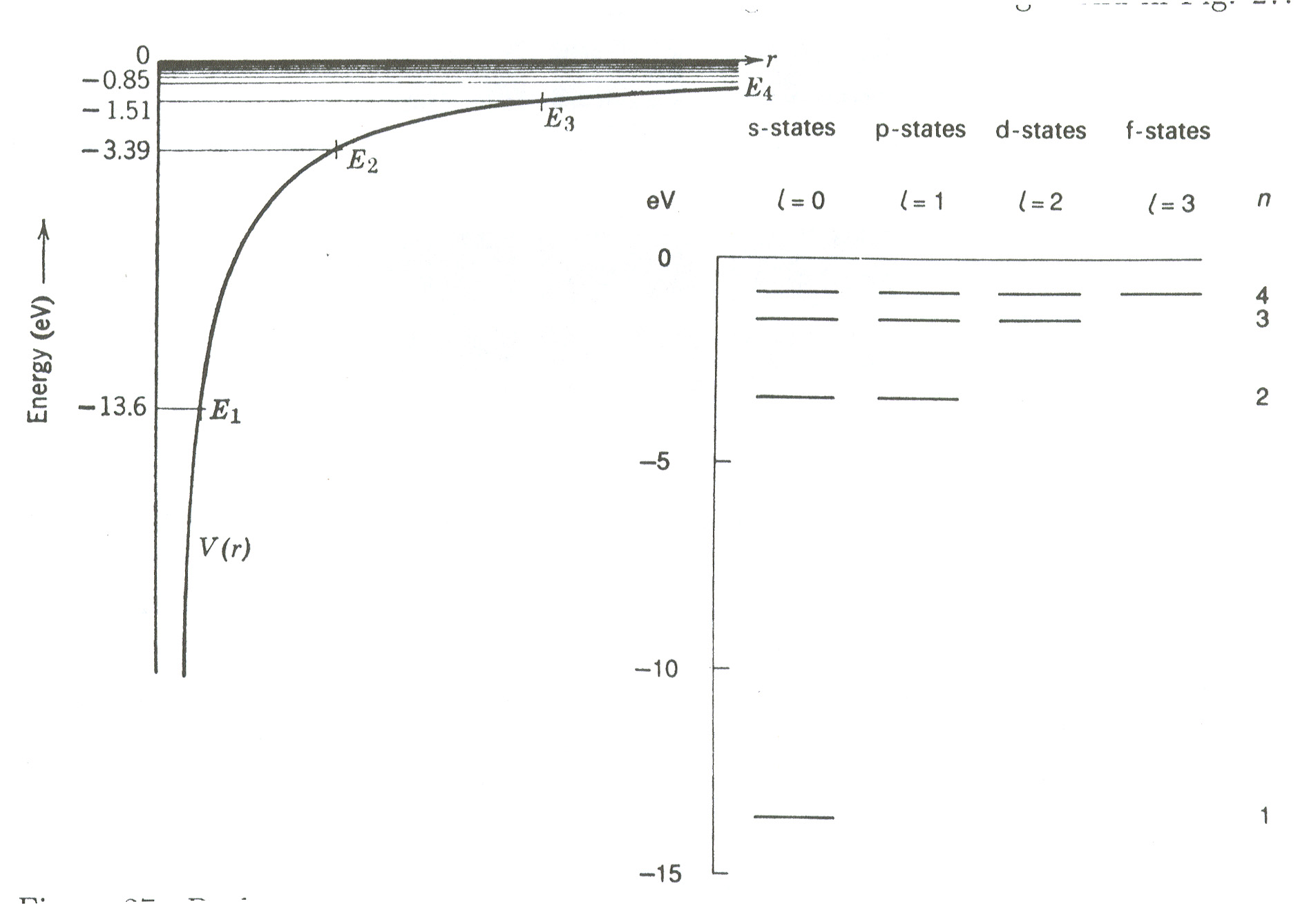
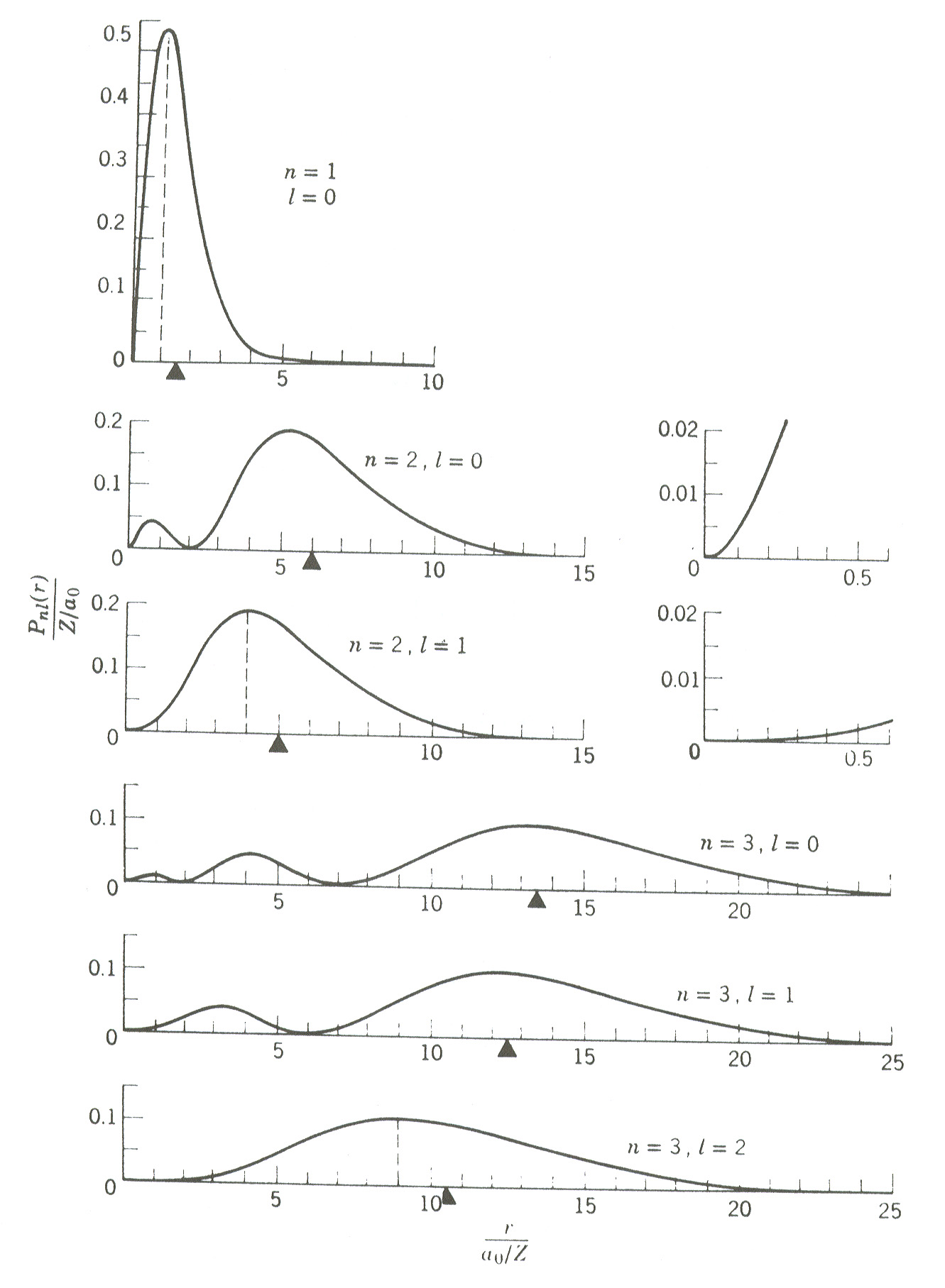
De laagste-orde radiële golffuncties van een één-elektron
atoom kunnen expliciet geschreven worden als
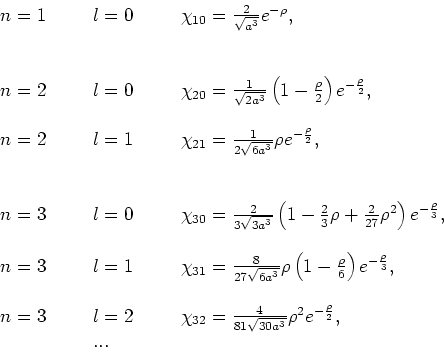 |
(259) |
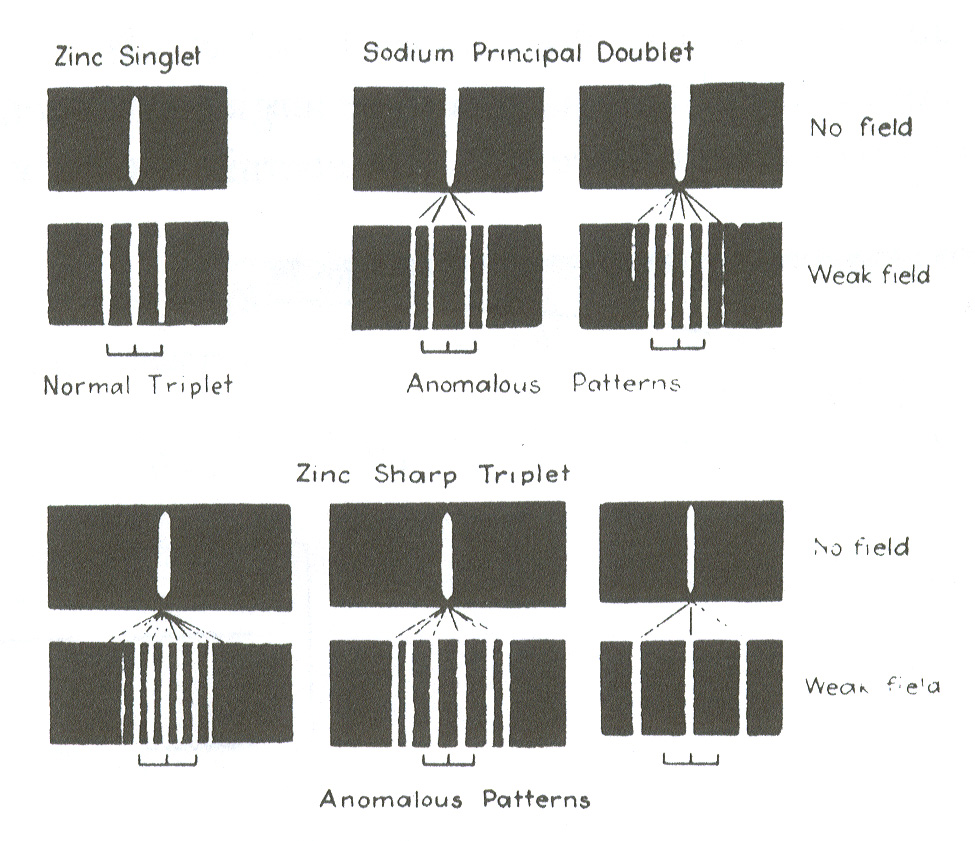
Tenslotte tonen we in Fig. 28 de experimentele observatie
van de opsplitsing van de spectraallijnen van diverse elementen
in een zwak magnetisch veld. Het verband tussen de structuur van de
multipletten en het periodiek systeem leidde tot de uiteindelijke
ontdekking van spin. Wolfgang Pauli kende deze eigenschap toe aan het
elektron, waarbij hij twee waarden van spin toeliet. Dit betekende
effectief het invoeren van een vierde quantumgetal in de beschrijving
van elk atomair elektron.