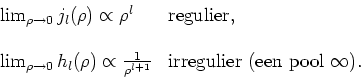Next: Deeltje in de Coulomb
Up: Operatoren voor Impulsmoment
Previous: Scheiden van Variabelen
We nemen aan dat ergens in het interval
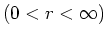 een gebied bestaat met een constante potentiaal,
een gebied bestaat met een constante potentiaal,
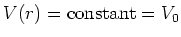 .
De radiële vergelijking neemt dan de volgende vorm aan
.
De radiële vergelijking neemt dan de volgende vorm aan
![\begin{displaymath}
\left[-{\hbar^2 \over 2m}{d^2 \over dr^2} + {l(l+1) \over 2mr^2}\hbar^2
+V_0 \right] y_l(r) = Ey_l(r) .
\end{displaymath}](img601.gif) |
(242) |
Voor de energie van het deeltje nemen we 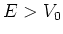 en definiëren
en definiëren
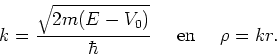 |
(243) |
Hiermee kunnen we de radiële vergelijking schrijven als
![\begin{displaymath}
\left[{d^2 \over d\rho^2} + \left( 1- {l(l+1) \over \rho^2}\right) \right]
y_l(\rho ) = 0 .
\end{displaymath}](img603.gif) |
(244) |
Oorspronkelijk hadden we voor de radiële golffunctie
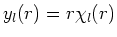 en we kunnen dus schrijven
en we kunnen dus schrijven
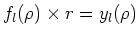 .
Aldus vinden we
.
Aldus vinden we
![\begin{displaymath}
\left[{d^2 \over d\rho^2} + {2 \over \rho}{d \over d\rho}+
\left( 1- {l(l+1) \over \rho^2}\right) \right] f_l(\rho ) = 0 .
\end{displaymath}](img605.gif) |
(245) |
Bovenstaande vergelijking staat in de functietheorie bekend als
de sferische Bessel differentiaalvergelijking, die als oplossingen de
sferische Besselfuncties heeft. De algemene oplossing van vergelijking
(245) is een lineaire combinatie van twee particuliere
oplossingen. De meest gebruikelijke particuliere oplossingen zijn
 |
(246) |
Fig. 24 toont enkele van de reguliere Besselfuncties.
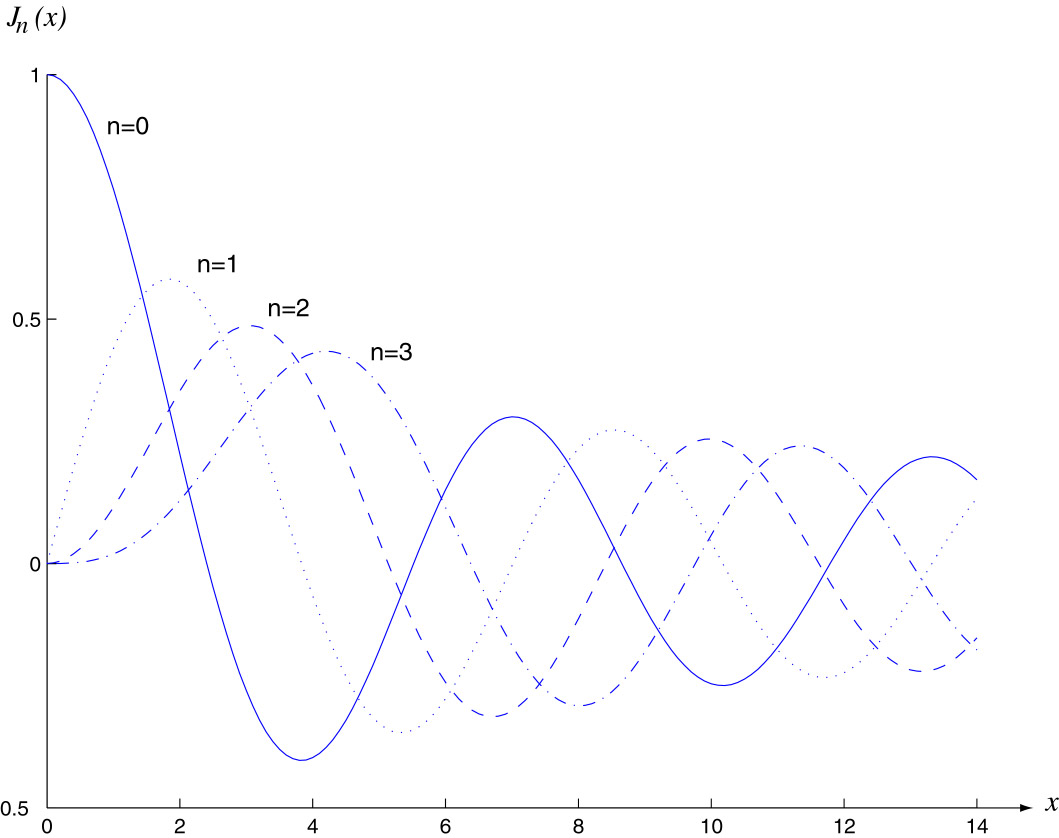 Figure 24:
Reguliere Besselfuncties die het radiële deel van
de golffunctie beschrijven van een deeltje dat zich in een constante
potentiaal beweegt.
Figure 24:
Reguliere Besselfuncties die het radiële deel van
de golffunctie beschrijven van een deeltje dat zich in een constante
potentiaal beweegt.
Deze functies zijn gedefinieerd als
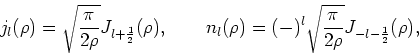 |
(247) |
en
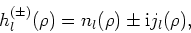 |
(248) |
met 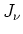 de normale Besselfunctie van de orde
de normale Besselfunctie van de orde 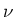 .
Merk op dat
.
Merk op dat 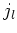 en
en 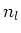 reëele functies zijn, terwijl
geldt dat
reëele functies zijn, terwijl
geldt dat
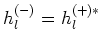 .
.
De laagste-orde Besselfuncties zijn
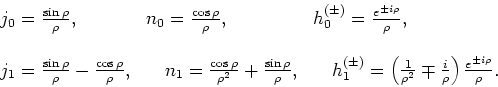 |
(249) |
Voor kleine 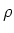 geldt
geldt
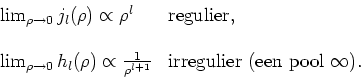 |
(250) |
De enige radiële functie die gebonden blijft als
 is de Hankelse functie
is de Hankelse functie 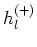 .
.
Tenslotte merken we op dat we nu ook een vergelijking kunnen vinden
voor de golffunctie van een vrij deeltje uitgedrukt in
sferische coördinaten. Er geldt onderstaande expansie van een
vlakke golf
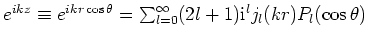 . . |
| |



Next: Deeltje in de Coulomb
Up: Operatoren voor Impulsmoment
Previous: Scheiden van Variabelen
Jo van den Brand
2000-10-21
![]() een gebied bestaat met een constante potentiaal,
een gebied bestaat met een constante potentiaal,
![]() .
De radiële vergelijking neemt dan de volgende vorm aan
.
De radiële vergelijking neemt dan de volgende vorm aan
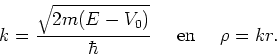

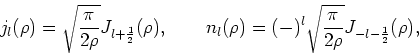
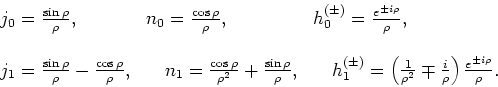
![]() geldt
geldt