


Next: Centrale Vierkante Potentiaal Put
Up: Operatoren voor Impulsmoment
Previous: Sferisch Harmonische Functies
We gaan nu proberen de Schrödingervergelijking in sferische
coördinaten op te lossen met behulp van de techniek van het scheiden
van variabelen. Hiertoe proberen we de oplossing
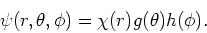 |
(223) |
We substitueren
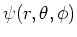 in de Schrödingervergelijking
in de Schrödingervergelijking
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {1 \over r^2}{\partial \over
\par...
...er \partial \theta} \right) \right]
+ V(r) \chi gh = E \chi gh
\end{displaymath}](img565.gif) |
(224) |
en kunnen dit herschrijven als
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {gh \over r^2}{{\rm d} \over
{\rm...
...r {\rm d} \theta} \right) \right]
+ V(r) \chi gh = E \chi gh .
\end{displaymath}](img566.gif) |
(225) |
We vermenigvuldigen de vergelijking met
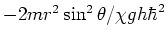 en krijgen
en krijgen
![\begin{displaymath}
{1 \over h}{{\rm d}^2 h \over {\rm d} \phi^2} =
{-\sin^2{\th...
...{2m \over \hbar^2}r^2 \sin^2{\theta}
\left[ E - V(r) \right] .
\end{displaymath}](img568.gif) |
(226) |
De linkerkant van bovenstaande vergelijking hangt niet af van 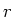 of
of
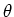 , terwijl de rechterzijde niet afhangt van
, terwijl de rechterzijde niet afhangt van 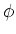 . De uitdrukkingen
aan beide kanten van het gelijkteken dienen derhalve gelijk te zijn
aan een constante. Hiervoor kiezen we
. De uitdrukkingen
aan beide kanten van het gelijkteken dienen derhalve gelijk te zijn
aan een constante. Hiervoor kiezen we 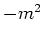 en verkrijgen
de volgende twee differentiaalvergelijkingen.
en verkrijgen
de volgende twee differentiaalvergelijkingen.
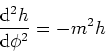 |
(227) |
en
![\begin{displaymath}
-{1 \over \chi} {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d...
...ar^2}r^2 \left[ E - V(r) \right]
= -{m^2 \over \sin{\theta}}.
\end{displaymath}](img571.gif) |
(228) |
De eerste vergelijking heeft als oplossing
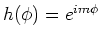 .
We dienen nu de eis te stellen dat de oplossing eenduidig
is, hetgeen van speciaal belang is voor de hoeken
.
We dienen nu de eis te stellen dat de oplossing eenduidig
is, hetgeen van speciaal belang is voor de hoeken
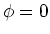 en
en 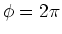 . We krijgen hiermee
. We krijgen hiermee
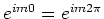 en dus
en dus
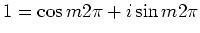 .
Aan deze eis kan enkel voldaan worden in geval
.
Aan deze eis kan enkel voldaan worden in geval
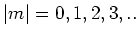 .
We herkennen in de oplossing voor de
.
We herkennen in de oplossing voor de 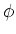 afhankelijkheid de
uitdrukking
afhankelijkheid de
uitdrukking 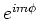 in de sferisch harmonische functies.
in de sferisch harmonische functies.
De tweede vergelijking kan herschreven worden tot
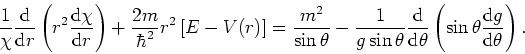 |
(229) |
In bovenstaande vergelijking zijn we er in geslaagd de variabelen
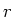 en
en 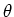 te scheiden. We voeren dan ook een scheidingsconstante
in en kiezen hiervoor
te scheiden. We voeren dan ook een scheidingsconstante
in en kiezen hiervoor 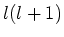 . We vinden dan de
twee differentiaalvergelijkingen
. We vinden dan de
twee differentiaalvergelijkingen
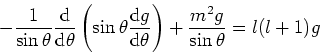 |
(230) |
en
![\begin{displaymath}
{1 \over r^2} {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} ...
... \hbar^2} \left[ E - V(r) \right] =
l(l+1) {\chi \over r^2} .
\end{displaymath}](img581.gif) |
(231) |
Als we de differentiaalvergelijking voor de 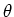 afhankelijkheid
oplossen15,
dan vinden we dat eindige oplossingen slechts
verkregen kunnen worden indien
afhankelijkheid
oplossen15,
dan vinden we dat eindige oplossingen slechts
verkregen kunnen worden indien
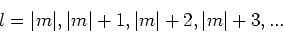 |
(236) |
Deze oplossingen kunnen geschreven worden als
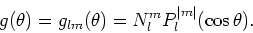 |
(237) |
We herkennen in de functies
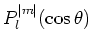 de
Legendre functies die polynomen zijn in
de
Legendre functies die polynomen zijn in 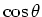 en waarvan de
vorm afhangt van de waarde van het quantumgetal
en waarvan de
vorm afhangt van de waarde van het quantumgetal 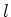 en de absolute
waarde van het quantumgetal
en de absolute
waarde van het quantumgetal 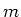 . Merk op dat
. Merk op dat 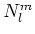 de
normalisatie constanten voorstellen.
de
normalisatie constanten voorstellen.
Samenvattend kunnen we de algemene oplossingen van de Schrödingervergelijking
voor een centrale potentiaal dus schrijven als
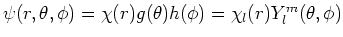 . . |
| |
Het radiële deel van de oplossing van de Schrödingervergelijking
voldoet aan
![\begin{displaymath}
\left[ {{\bf p_r}^2 \over 2m} + {l(l+1) \over 2mr^2}\hbar^2 +V(r) -E \right]
\chi_l(r) = 0 ,
\end{displaymath}](img591.gif) |
(238) |
waarbij
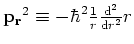 .
We nemen aan dat de radiële golffunctie geschreven kan worden
als
.
We nemen aan dat de radiële golffunctie geschreven kan worden
als
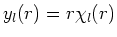 en vinden door substitutie in vergelijking
(238)
en vinden door substitutie in vergelijking
(238)
![\begin{displaymath}
\left[-{\hbar^2 \over 2m}{d^2 \over dr^2} + {l(l+1) \over 2mr^2}\hbar^2
+V(r) -E \right] y_l(r) = 0 .
\end{displaymath}](img594.gif) |
(239) |
Uit de hermiticiteitseis voor 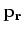 kan afgeleid worden dat
kan afgeleid worden dat
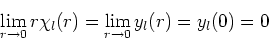 |
(240) |
dient te gelden
Na het scheiden van de variabelen vinden we voor de golffunctie
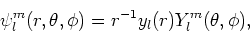 |
(241) |
waarbij 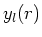 de oplossing is van de radiële vergelijking
met
de oplossing is van de radiële vergelijking
met 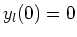 . Verder dient de functie
. Verder dient de functie 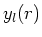 begrensd te zijn.
begrensd te zijn.



Next: Centrale Vierkante Potentiaal Put
Up: Operatoren voor Impulsmoment
Previous: Sferisch Harmonische Functies
Jo van den Brand
2000-10-21
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {1 \over r^2}{\partial \over
\par...
...er \partial \theta} \right) \right]
+ V(r) \chi gh = E \chi gh
\end{displaymath}](img565.gif)
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {gh \over r^2}{{\rm d} \over
{\rm...
...r {\rm d} \theta} \right) \right]
+ V(r) \chi gh = E \chi gh .
\end{displaymath}](img566.gif)
![\begin{displaymath}
{1 \over h}{{\rm d}^2 h \over {\rm d} \phi^2} =
{-\sin^2{\th...
...{2m \over \hbar^2}r^2 \sin^2{\theta}
\left[ E - V(r) \right] .
\end{displaymath}](img568.gif)
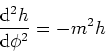
![\begin{displaymath}
-{1 \over \chi} {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d...
...ar^2}r^2 \left[ E - V(r) \right]
= -{m^2 \over \sin{\theta}}.
\end{displaymath}](img571.gif)
![]() .
We dienen nu de eis te stellen dat de oplossing eenduidig
is, hetgeen van speciaal belang is voor de hoeken
.
We dienen nu de eis te stellen dat de oplossing eenduidig
is, hetgeen van speciaal belang is voor de hoeken
![]() en
en ![]() . We krijgen hiermee
. We krijgen hiermee
![]() en dus
en dus
![]() .
Aan deze eis kan enkel voldaan worden in geval
.
Aan deze eis kan enkel voldaan worden in geval
![]() .
We herkennen in de oplossing voor de
.
We herkennen in de oplossing voor de ![]() afhankelijkheid de
uitdrukking
afhankelijkheid de
uitdrukking ![]() in de sferisch harmonische functies.
in de sferisch harmonische functies.
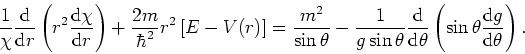
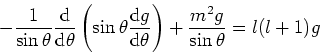
![\begin{displaymath}
{1 \over r^2} {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} ...
... \hbar^2} \left[ E - V(r) \right] =
l(l+1) {\chi \over r^2} .
\end{displaymath}](img581.gif)
![]() afhankelijkheid
oplossen15,
dan vinden we dat eindige oplossingen slechts
verkregen kunnen worden indien
afhankelijkheid
oplossen15,
dan vinden we dat eindige oplossingen slechts
verkregen kunnen worden indien