


Next: Scheiden van Variabelen
Up: Operatoren voor Impulsmoment
Previous: Operatoren voor Impulsmoment
De sferisch harmonische functies
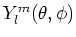 zijn de gemeenschappelijke eigenfuncties van de operatoren
zijn de gemeenschappelijke eigenfuncties van de operatoren
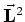 en
en 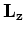 .
.
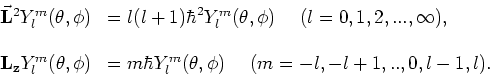 |
(215) |
Bovenstaande eigenwaardenvergelijkingen hebben slechts eindige
en eenduidige eigenfuncties voor bepaalde eigenwaarden,
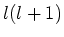 voor
voor 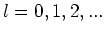 . De eigenwaarde
. De eigenwaarde 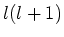 is
is
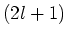 -voudig ontaard. Dit betekent dat er
-voudig ontaard. Dit betekent dat er 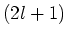 lineair onafhankelijke functies bestaan die eigenfunctie zijn van
de operator
lineair onafhankelijke functies bestaan die eigenfunctie zijn van
de operator 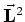 behorende bij de eigenwaarde
behorende bij de eigenwaarde
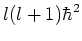 . Deze eigenfuncties worden aangegeven door de
sferisch harmonische functies
. Deze eigenfuncties worden aangegeven door de
sferisch harmonische functies
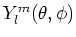 met
met
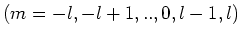 .
.
Anders geformuleerd kunnen we stellen dat de eigenwaardenvergelijkingen
(215) de quantisatie van het impulsmoment uitdrukken:
de kwadratische grootte van het impulsmoment 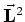 van
een deeltje kan slechts één van de discrete set van waarden
van
een deeltje kan slechts één van de discrete set van waarden
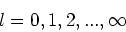 |
(216) |
aannemen, terwijl de 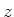 -component van het impulsmoment
-component van het impulsmoment 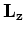 van
een deeltje slechts een van de discrete waarden
van
een deeltje slechts een van de discrete waarden
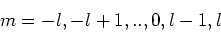 |
(217) |
kan aannemen.
We noemen 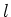 het quantumgetal voor het impulsmoment en
het quantumgetal voor het impulsmoment en 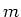 het
magnetische quantumgetal. Toestanden met
het
magnetische quantumgetal. Toestanden met 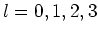 worden
worden
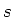 -,
-, 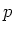 -,
-, 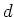 -,
-, 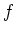 -toestanden genoemd. Voor toestanden met
-toestanden genoemd. Voor toestanden met 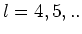 gaat de aanduiding alfabetisch verder met
gaat de aanduiding alfabetisch verder met 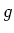 ,
, 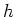 , enzovoort. Dit
noemt men de spectroscopische notatie.
, enzovoort. Dit
noemt men de spectroscopische notatie.
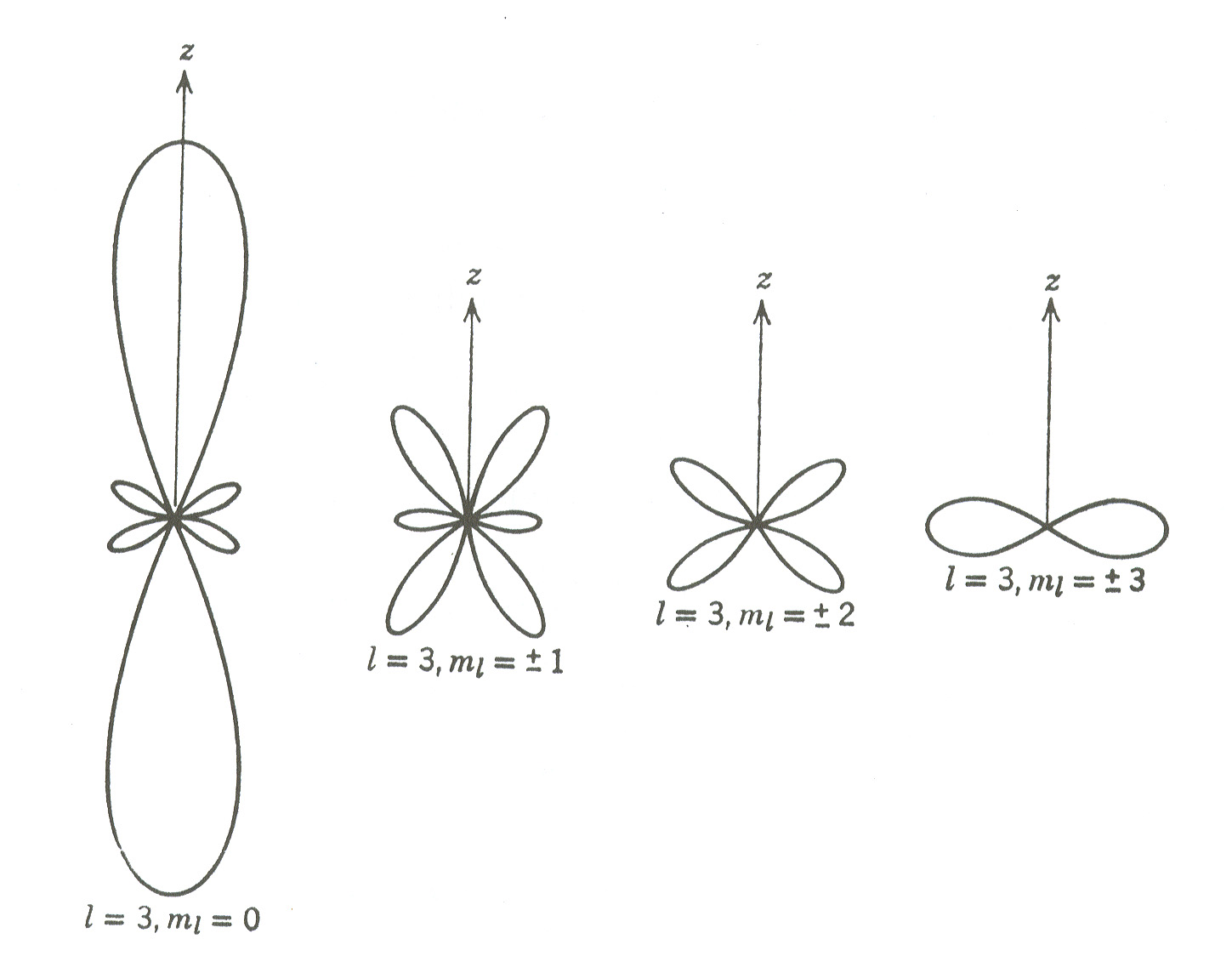 Figure 21:
Polaire diagrammen van de ruimtelijke afhankelijkheid
van de waarschijnlijkheidsdichtheden van het waterstofatoom voor
Figure 21:
Polaire diagrammen van de ruimtelijke afhankelijkheid
van de waarschijnlijkheidsdichtheden van het waterstofatoom voor
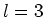 ;
;
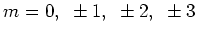 .
.
De waarschijnlijkheidsdichtheden van de diverse toestanden worden
gegeven door
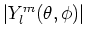 en de polaire verdelingen
worden getoond in Fig. 21 voor het geval
en de polaire verdelingen
worden getoond in Fig. 21 voor het geval
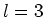 ;
;
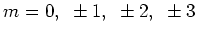 .
.
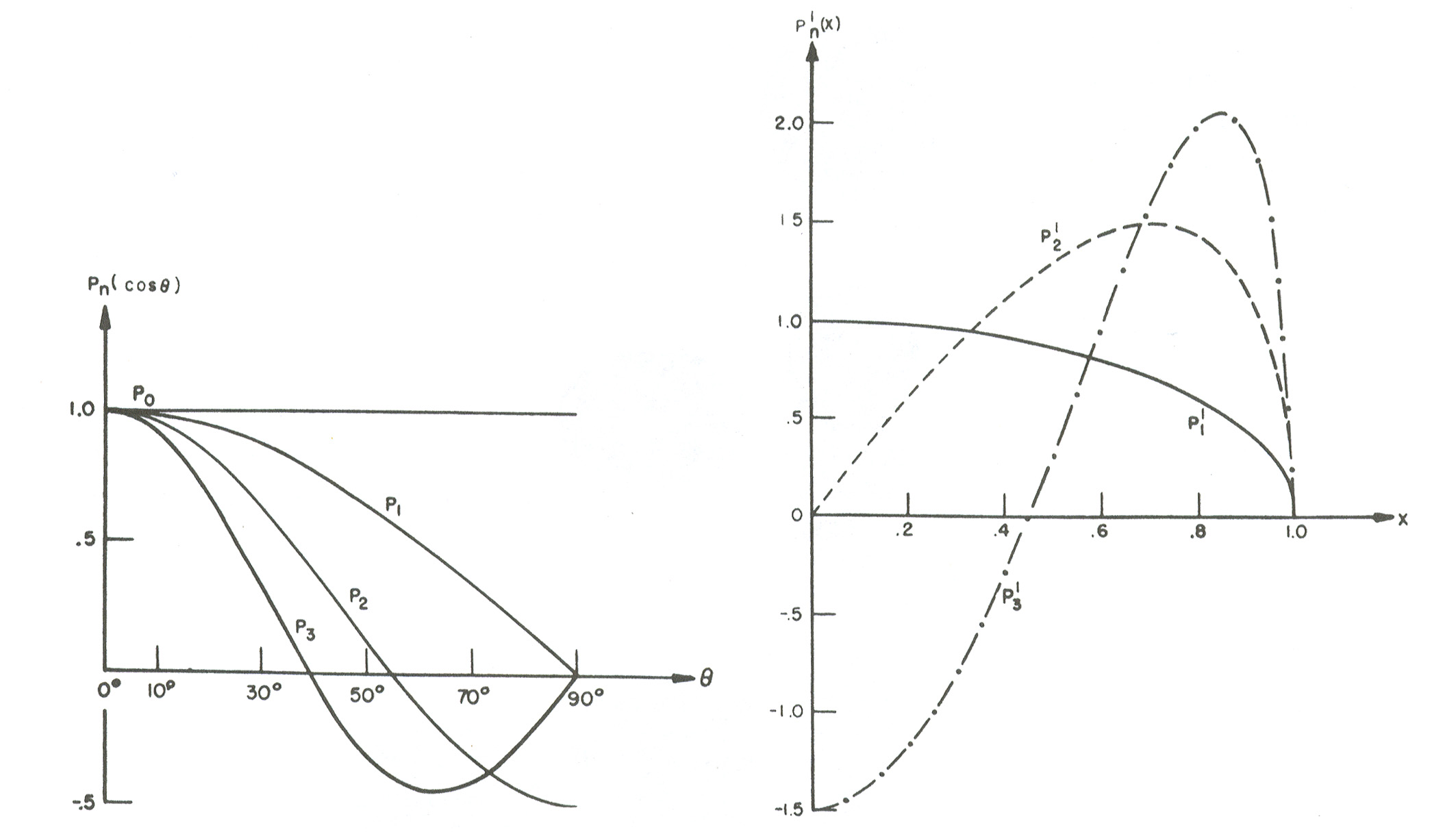 Figure 22:
Enkele Legendre polynomen die de
Figure 22:
Enkele Legendre polynomen die de  afhankelijkheid
van de golffunctie in een sferisch coördinatenstelsel beschrijven.
afhankelijkheid
van de golffunctie in een sferisch coördinatenstelsel beschrijven.
De functies
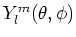 kunnen expliciet geschreven worden als
kunnen expliciet geschreven worden als
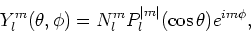 |
(218) |
met
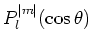 de geassocieerde Legendre
functies en
de geassocieerde Legendre
functies en 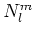 een set normalisatie constanten.
Enkele van de Legendre polynomen die de
een set normalisatie constanten.
Enkele van de Legendre polynomen die de 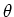 afhankelijkheid
van de golffunctie in een sferisch coördinatenstelsel beschrijven
worden getoond in Fig. 22. De geassocieerde
Legendre functie worden gedefinieerd door de vergelijking
afhankelijkheid
van de golffunctie in een sferisch coördinatenstelsel beschrijven
worden getoond in Fig. 22. De geassocieerde
Legendre functie worden gedefinieerd door de vergelijking
![\begin{displaymath}
P_l^{\vert m \vert} (\mu ) = {1 \over 2^ll!} (1-\mu^2 )^{\ve...
... m \vert} \over {\rm d}\mu^{l+ \vert m \vert}}
[(\mu^2 -1)^l]
\end{displaymath}](img557.gif) |
(219) |
en de normalisatie constanten door
![\begin{displaymath}
N_l^m = (-1)^{(m+\vert m \vert )/2} \left[ {2l+1 \over 4\pi}
{(l-\vert m \vert )! \over (l+\vert m \vert )!} \right]^{1/2} .
\end{displaymath}](img558.gif) |
(220) |
De laagste-orde sferisch harmonische functies worden gegeven door
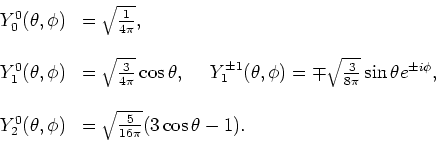 |
(221) |
 Figure 23:
De sferisch harmonische functies
Figure 23:
De sferisch harmonische functies
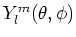 voor de laagste waarden van
voor de laagste waarden van 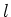 en
en 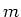 .
.
In Fig. 23 zijn de sferisch harmonische functies
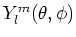 geplot voor de laagste waarden van
geplot voor de laagste waarden van 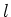 en
en 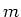 .
De figuur toont de functie
.
De figuur toont de functie
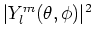 in
sferische coördinaten. Voor een gegeven richting van
in
sferische coördinaten. Voor een gegeven richting van 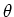 en
en 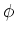 in het coördinatenstelsel, is de afstand van het oppervlak
tot de oorsprong zijn gelijk aan het kwadraat van de sferisch harmonische
functiewaarde.
De sferisch harmonische functies
in het coördinatenstelsel, is de afstand van het oppervlak
tot de oorsprong zijn gelijk aan het kwadraat van de sferisch harmonische
functiewaarde.
De sferisch harmonische functies
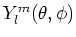 zijn in de
functieruimte van de kwadratisch integreerbare functies gedefinieerd
op de eenheidsbol. De functies voldoen aan orthogonaliteit. Er geldt
zijn in de
functieruimte van de kwadratisch integreerbare functies gedefinieerd
op de eenheidsbol. De functies voldoen aan orthogonaliteit. Er geldt
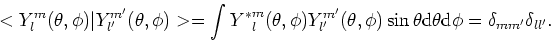 |
(222) |



Next: Scheiden van Variabelen
Up: Operatoren voor Impulsmoment
Previous: Operatoren voor Impulsmoment
Jo van den Brand
2000-10-21
![]() zijn de gemeenschappelijke eigenfuncties van de operatoren
zijn de gemeenschappelijke eigenfuncties van de operatoren
![]() en
en ![]() .
.
![]() van
een deeltje kan slechts één van de discrete set van waarden
van
een deeltje kan slechts één van de discrete set van waarden

![]() en de polaire verdelingen
worden getoond in Fig. 21 voor het geval
en de polaire verdelingen
worden getoond in Fig. 21 voor het geval
![]() ;
;
![]() .
.

![]() kunnen expliciet geschreven worden als
kunnen expliciet geschreven worden als
![\begin{displaymath}
P_l^{\vert m \vert} (\mu ) = {1 \over 2^ll!} (1-\mu^2 )^{\ve...
... m \vert} \over {\rm d}\mu^{l+ \vert m \vert}}
[(\mu^2 -1)^l]
\end{displaymath}](img557.gif)
![\begin{displaymath}
N_l^m = (-1)^{(m+\vert m \vert )/2} \left[ {2l+1 \over 4\pi}
{(l-\vert m \vert )! \over (l+\vert m \vert )!} \right]^{1/2} .
\end{displaymath}](img558.gif)
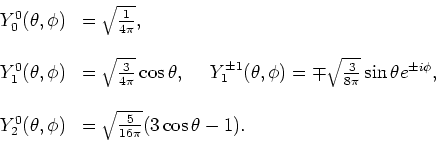

![]() geplot voor de laagste waarden van
geplot voor de laagste waarden van ![]() en
en ![]() .
De figuur toont de functie
.
De figuur toont de functie
![]() in
sferische coördinaten. Voor een gegeven richting van
in
sferische coördinaten. Voor een gegeven richting van ![]() en
en ![]() in het coördinatenstelsel, is de afstand van het oppervlak
tot de oorsprong zijn gelijk aan het kwadraat van de sferisch harmonische
functiewaarde.
De sferisch harmonische functies
in het coördinatenstelsel, is de afstand van het oppervlak
tot de oorsprong zijn gelijk aan het kwadraat van de sferisch harmonische
functiewaarde.
De sferisch harmonische functies
![]() zijn in de
functieruimte van de kwadratisch integreerbare functies gedefinieerd
op de eenheidsbol. De functies voldoen aan orthogonaliteit. Er geldt
zijn in de
functieruimte van de kwadratisch integreerbare functies gedefinieerd
op de eenheidsbol. De functies voldoen aan orthogonaliteit. Er geldt