


Next: Sferisch Harmonische Functies
Up: LES 05
Previous: Wiskundig Intermezzo
We weten uit de klassieke mechanica dat het impulsmoment van
een deeltje gedefinieerd is als
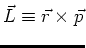 en we construeren daarom de quantummechanische operator op analoge wijze
en we construeren daarom de quantummechanische operator op analoge wijze
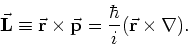 |
(193) |
In een cartesisch coördinatensysteem kunnen de operatoren voor de
drie componenten van het impulsmoment van een deeltje geschreven
worden als
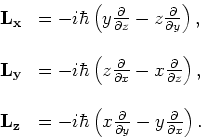 |
(194) |
In een sferisch coördinatenstelsel hebben de operatoren de
volgende vorm
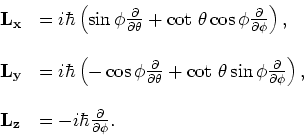 |
(195) |
We zullen tonen dat de uitdrukkingen (194)
en (195) equivalent zijn. Hiervoor maken we gebruik van
de relaties (184). Er geldt
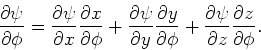 |
(196) |
We vinden met behulp van de relaties (184)
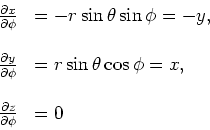 |
(197) |
en dus
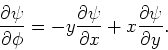 |
(198) |
We kunnen dit schrijven als een operatorvergelijking en vinden
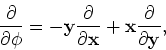 |
(199) |
waarmee we de equivalentie hebben aangetoond van de twee uitdrukkingen
voor 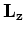 gegeven in vergelijking (194) en
(195). De uitdrukkingen voor
gegeven in vergelijking (194) en
(195). De uitdrukkingen voor 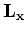 en
en 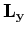 kunnen op analoge wijze afgeleid worden13.
kunnen op analoge wijze afgeleid worden13.
In cartesische coördinaten kan de operator voor het kwadraat van
de grootte van het impulsmoment gevonden worden uit
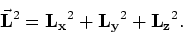 |
(202) |
We kunnen de uitdrukking voor 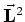 in een sferisch stelsel
vinden met enige algebra en krijgen
in een sferisch stelsel
vinden met enige algebra en krijgen
![\begin{displaymath}
{\bf\vec L}^2 = -\hbar^2 \left[ {1 \over \sin{\theta}}{\part...
...er \sin^2{\theta}}{\partial^2 \over \partial \phi^2} \right] .
\end{displaymath}](img516.gif) |
(203) |
Merk op dat we hier de vorm herkennen van de tweede en derde term
in uitdrukking (183)
voor de Laplace operator in sferische coördinaten.
Vervolgens gebruiken we een stelling voor vectoren14, waarbij
het uitproduct van twee vectoren geschreven kan worden als
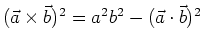 ,
en we passen deze stelling toe op de norm van de operator van het impulsmoment.
We vinden nu de belangrijke operatorvergelijking
,
en we passen deze stelling toe op de norm van de operator van het impulsmoment.
We vinden nu de belangrijke operatorvergelijking
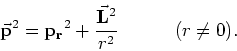 |
(205) |
We kunnen de Schrödingervergelijking in sferische coördinaten
schrijven als
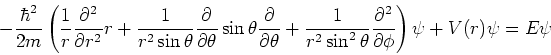 |
(206) |
en kunnen dit met behulp van vergelijkingen (203)
en (208) beknopter weergeven als
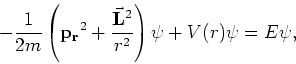 |
(207) |
waarbij 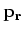 de radiële component is van de
impulsoperator in sferische coördinaten. We hebben
de radiële component is van de
impulsoperator in sferische coördinaten. We hebben
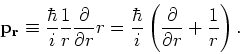 |
(208) |
We zullen nu de operatoren voor het impulsmoment van een
deeltje nader beschouwen. We zien in vergelijking (194)
dat de componenten zijn uitgebouwd uit commuterende hermitische
operatoren. Daarom zal 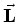 ook hermitisch zijn. We kunnen
nu de commutatierelaties uitrekenen voor de componenten van de
operator voor het impulsmoment. We vinden
ook hermitisch zijn. We kunnen
nu de commutatierelaties uitrekenen voor de componenten van de
operator voor het impulsmoment. We vinden
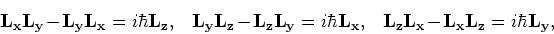 |
(209) |
We kunnen dit afkorten tot
![\begin{displaymath}
{\bf\vec L \times \vec L} = i\hbar{\bf\vec L},
~~~~{\rm of~ook~als}~~~~
[{\bf L_i,L_j}] = i\hbar \epsilon_{ijk} {\bf L_k}.
\end{displaymath}](img530.gif) |
(210) |
Hierbij is
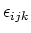 de volledig antisymmetrische tensor in
drie dimensies gegeven door
de volledig antisymmetrische tensor in
drie dimensies gegeven door
 |
(211) |
Dit betekent dat de componenten van het impulsmoment van een
deeltje niet allemaal op dezelfde tijd meetbaar zijn. De operator van
het kwadraat van het impulsmoment van een deeltje commuteert met
alle componenten van de operator van het impulsmoment. Er geldt
![\begin{displaymath}[{\bf\vec L^2,L_x}]= [{\bf\vec L^2,L_y}] = [{\bf\vec L^2,L_z}] = 0.
\end{displaymath}](img533.gif) |
(212) |
De operator voor impulsmoment commuteert ook met de hamiltoniaan en er geldt dus
![\begin{displaymath}[ {\bf\vec L},{\bf H} ]=0 .
\end{displaymath}](img534.gif) |
(213) |
Verder weten we dat de hamiltoniaan opgebouwd is uit de operatoren
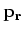 en
en 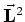 , en commuteert met de operatoren
, en commuteert met de operatoren
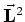 en
en 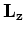 . Er geldt
. Er geldt
![\begin{displaymath}[ {\bf H}, {\bf\vec L}^2 ]=0 ~~~~~{\rm en}~~~~
[ {\bf H}, {\bf\vec L_z} ] =0 .
\end{displaymath}](img535.gif) |
(214) |
We hebben hiermee dus minstens een gemeenschappelijke basis voor
 ,
, 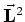 en
en 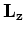 .
.
Subsections



Next: Sferisch Harmonische Functies
Up: LES 05
Previous: Wiskundig Intermezzo
Jo van den Brand
2000-10-21
![]() en we construeren daarom de quantummechanische operator op analoge wijze
en we construeren daarom de quantummechanische operator op analoge wijze
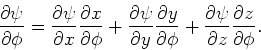
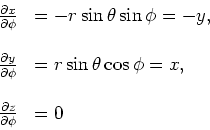
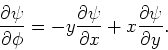
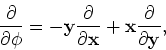
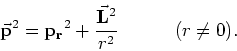
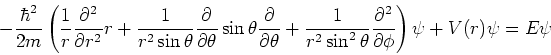
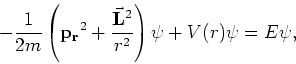
![]() ook hermitisch zijn. We kunnen
nu de commutatierelaties uitrekenen voor de componenten van de
operator voor het impulsmoment. We vinden
ook hermitisch zijn. We kunnen
nu de commutatierelaties uitrekenen voor de componenten van de
operator voor het impulsmoment. We vinden
