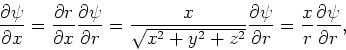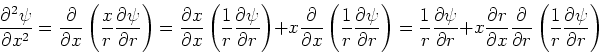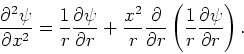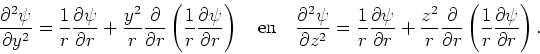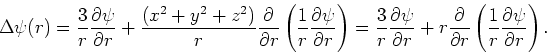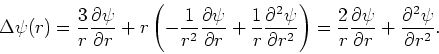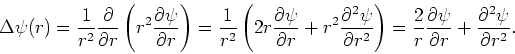Next: Operatoren voor Impulsmoment
Up: LES 05
Previous: LES 05
De Laplace operator is een ingrediënt van de Schrödingervergelijking
en wordt in een cartesisch coördinatensysteem geschreven als
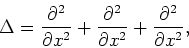 |
(182) |
terwijl in een sferisch coördinatensysteem geldt dat
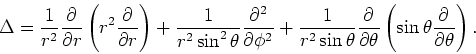 |
(183) |
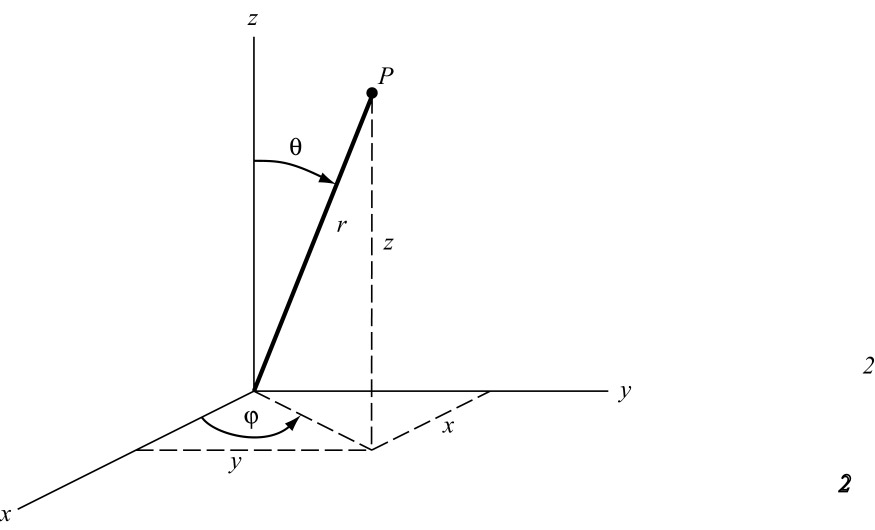 Figure 20:
De sferische coördinaten
Figure 20:
De sferische coördinaten 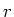 ,
, 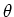 en
en 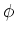 van een punt
van een punt 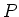 en de bijbehorende cartesische coördinaten
en de bijbehorende cartesische coördinaten
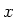 ,
, 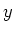 en
en 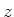 .
.
De coördinaten in beide stelsels staan met elkaar in verband
volgens
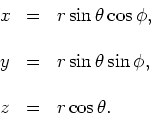 |
(184) |
Verder geldt de relatie
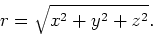 |
(185) |
We kunnen de eerste term van de Laplace operator in sferische
coördinaten vinden door aan te nemen dat de golffunctie
enkel een functie is van 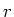 en dus geldt
en dus geldt
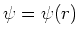 .
Met behulp van de kettingregel vinden we dan
.
Met behulp van de kettingregel vinden we dan
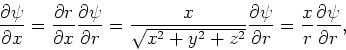 |
(186) |
terwijl voor de tweede-orde afgeleide geldt
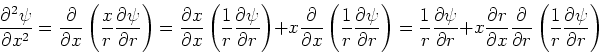 |
(187) |
en dus
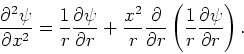 |
(188) |
Op dezelfde manier kunnen we de afgeleiden naar 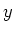 en
en 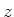 uitrekenen
en vinden
uitrekenen
en vinden
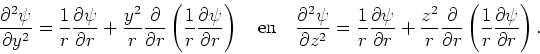 |
(189) |
Als we de laatste drie vergelijkingen optellen, dan vinden we
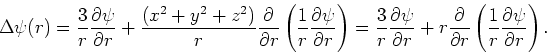 |
(190) |
We kunnen bovenstaande vergelijking omschrijven tot
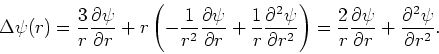 |
(191) |
Hiermee hebben we de eerste term van de Laplace operator in sferische
coördinaten gevonden. In de afleiding hebben we aangenomen dat
de golffunctie enkel een functie is van 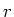 , dus geldt
, dus geldt
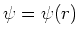 .
Merk op dat
.
Merk op dat
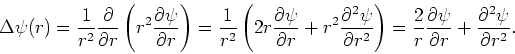 |
(192) |
De tweede en derde term in de uitdrukking voor de Laplace operator
in sferische coördinaten kunnen we vinden door eerst
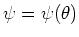 en vervolgens
en vervolgens
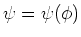 aan te nemen. We zullen in het
vervolg echter een andere manier gebruiken om ons doel te bereiken.
aan te nemen. We zullen in het
vervolg echter een andere manier gebruiken om ons doel te bereiken.



Next: Operatoren voor Impulsmoment
Up: LES 05
Previous: LES 05
Jo van den Brand
2000-10-21