


Next: Plausibiliteitsargumenten en Schrödingervergelijking
Up: Wiskundig Intermezzo
Previous: Complexe Grootheden
We merken op dat de golffunctie
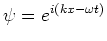 een complexe
functie is met een reëel en een imaginair deel. De
waarschijnlijkheidsdichtheid wordt gegeven door
een complexe
functie is met een reëel en een imaginair deel. De
waarschijnlijkheidsdichtheid wordt gegeven door
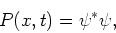 |
(93) |
waarbij 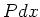 de kans voorstelt dat het deeltje wordt
aangetroffen7 in het
interval
de kans voorstelt dat het deeltje wordt
aangetroffen7 in het
interval 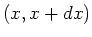 .
.
We normeren de golffunctie van een deeltje zo, dat geldt
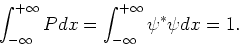 |
(94) |
De verwachtingswaarde 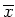 van de positie is
van de positie is
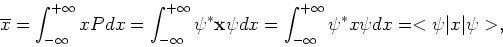 |
(95) |
terwijl voor elke observabele 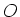 geldt dat zijn verwachtingswaarde
geldt dat zijn verwachtingswaarde 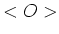 gegeven is door
gegeven is door
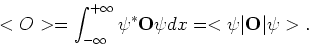 |
(96) |
Jo van den Brand
2000-10-21
![]() een complexe
functie is met een reëel en een imaginair deel. De
waarschijnlijkheidsdichtheid wordt gegeven door
een complexe
functie is met een reëel en een imaginair deel. De
waarschijnlijkheidsdichtheid wordt gegeven door