Variation of the Fundamental Constants of Nature ?

Here follow some notes and references to the study material for this course. Some of it is meant as study material, other parts have the purpose of background material.

As for the leading paper for this course we choose:
"The Fundamental constants and their variation: observational and theoretical status" by Jean-Philippe Uzan, which appeared as Reviews of Modern Physics 75, 403-455 (2003); click the link to attain access.
Note that while studying this paper, we will focus mainly on the electromagnetic aspects of the problem (i.e. in particular the physics of the quantum level structure of atoms and molecules), while we will not dig into the aspects of General Relativity, which are beyond the scope of the course.
For a more popular 'easy-reading' story on the topic of the course the student is referred to the book by John Barrow: The Constants of Nature.

    I. Theoretical Frameworks for Varying Constants

    Kaluza-Klein theories
      Already in the 1920s Theodore Kaluza and Oskar Klein (Klein's original Paper from 1926; background material) devised theories in attempts to unify electromagnetism and gravity (general relativity). For this purpose they started from higher-dimensional space-time; Klein defined the 5-th dimension having the topology of the circle on a hose-pipe, which may be compact, and therefore not observed. Kaluza and Klein did not themselves devise theories of varying constants, but it was shown that values for the fundamental constants (like the fine sructure consant alpha) depend on the compactification of the extra dimensions.

        Th. Kaluza and O. Klein
      The effects of the 5-th (and higher) dimension(s) and the specifics of compactification were later dealt with in a large number of papers, appearing to this date. Note that the KK-method with 4+D cosmologies deals with classical fields.

    Diracs Large Number Hypothesis
      Diracs theory on "Large Numbers" is phenomenological, numerological, and from a philosophical point of view also teleological. His theory of the Large Number Hypothesis (LNH) was laid down in a paper, written on his honeymoon (Dirac, Nature 1937).

        Paul Dirac
      He noted that three numbers that connected properties of elementary matter and those of the Universe:
      N1 = Size of the observable Universe / Electron radius = ct/(e2/mec2) = 1040
      N2 = Electromagnetic Force/ Gravitational Force = N2 = e2/GmeMp) = 1040
      N = Number of protons in the observable universe = c3t/GMp = 1080
      where the actual values are those estimated for the present day. The LNH may be stated as: "Any two of the very large dimensionless numbers occurring in Nature are connected by a simple mathematical relation, in which the coefficients are of order unity". Dirac hypothesized further that these large numbers should retain the same proportionality over time: N1 = N2 = sqrt (N) from which one can deduce the constraint:
      e2/Gmp ~ t, which led Dirac to conclude that the gravitational constant may have varied over time: G ~ 1/t.
      The LNH was criticised by many physicists (where the paleological argument in the Paper by Teller of 1948 is interesting to follow) and led Gamov (see Paper Gamov) to hypothesize: e2 ~ t.
      The LNH has remained a source of inspiration for the field and many modern theories pay tribute to it.
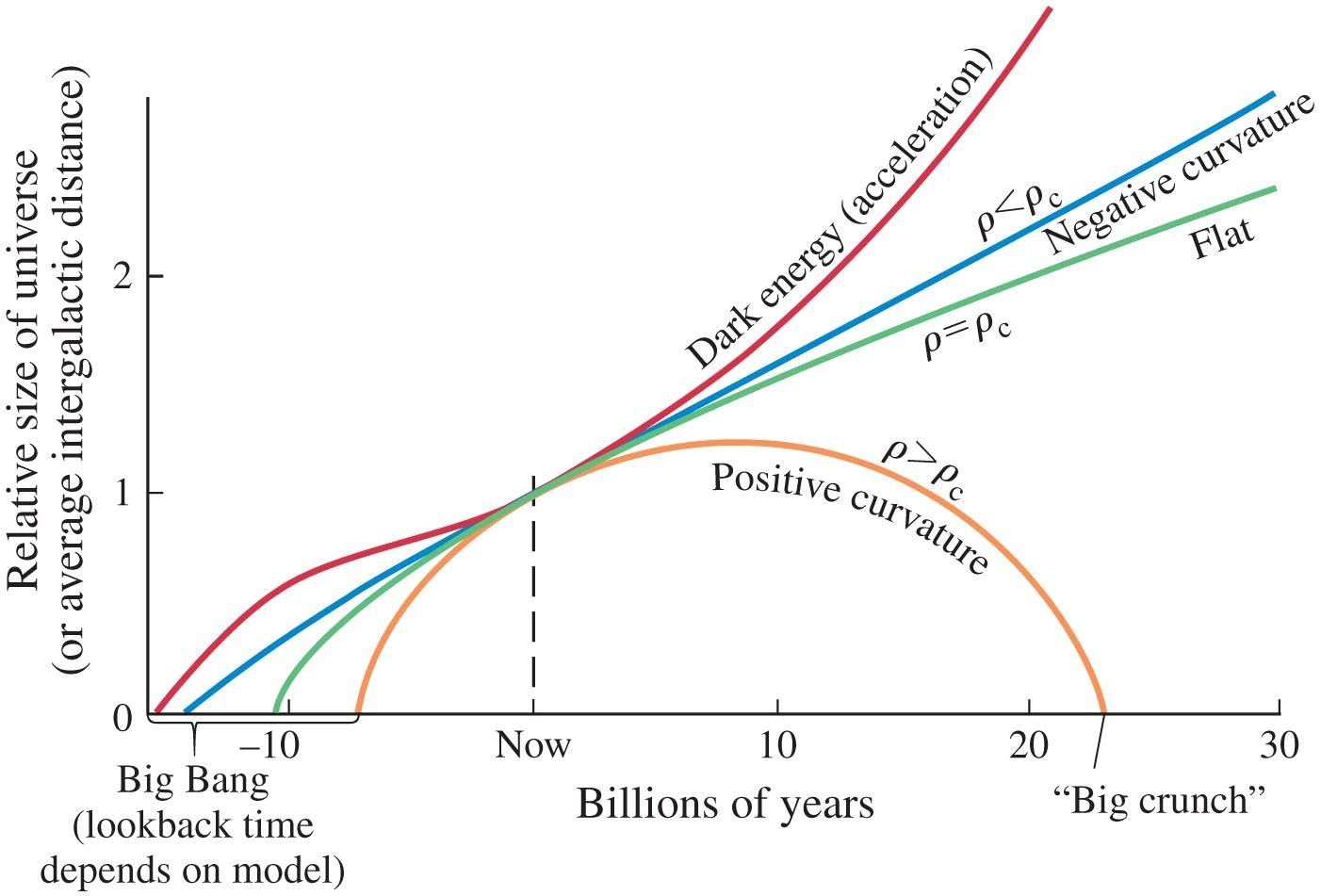
      Even the phenomenon of the increasingly expanding Universe, which may be described as due to Dark Energy, or to a 'repelling force' represented by the cosmological constant Lambda (which becomes a dynamical variable), may be viewed as a phenomenon of a varying gravitational force, in the spirit of the LNH.

    Quantum Field Theories
      The hypothesis that dimensionless constants like alpha and mu might be subject to change in principle implies that the energy level structure of matter (in the form of atoms, molecules, solids and fluids) undergo a temporal change. In the most simple picture this would imply non-conservation of energy. For this reason additional fields are invoked in quantum field theories of matter to compensate for this, leading to 'scalar fields' or the 'dilaton field'. For such theories to remain consistent, and to be consistent with physical observations of all kinds, certain limitations and constraints upon the dilaton field must be imposed. Such theories were explored by Bekenstein (see Paper Bekenstein). Many of the subsequent models devised built further on the ideas laid down in this paper.
      This concept was further elaborated, also including gravitation into the model, by Barrow, Sandvik, and Mageijo in a sequence of papers. In those papers constraints on the variation of various constants (in particular the fine structure constant alpha) were derived.

    (Super) String Theories
      One of the predictions of string theories, that have been proposed in a wide variety, is the existence of a dilaton field, an additional scalar filed that couples to matter. Superstring theories offer a theoretical framework where fundamental constants become expectation values of some fields.

    Chameleon Theories
      This entails a special set of theories that predict that the values of the coupling parameters depend on the local density of matter. It is described in papers by Khoury and Weltman:
      Chameleon Fields.
      Chameleon Cosmology.

    II. Fundamental Constants

    System of Units (SI)
      The fundamental constants of nature are related to the fundamental units, which are defined with respect to a method of realization. These issues are described in a recent paper by Peik (2010): Fundamental constants and units.

    Reduction to Natural units and dimensionless constants
      There is a discussion on which constants are fundamental, how fundamental constants can be represented in natural combinations (e.g. the Planck scales), and whether or not only dimensionless constants can be tested for their time variability. For this we refer to a Trialogue by Duff/Okun/Venziano and some further comments by Duff:
      Duff-Okun-Veneziano-trialogue.
      Duff-comment-2004.
      What we can learn from these discussions is that an experimental search for varying constants can only be made operational and can lead to a meaningful interpretation if the target is a dimensionless constant. If a variation in alpha would be detected than it would be a meaningless question to ask whether e, c or h would be varying. In the same fashion the interesting experiment using GPS and clocks, as published in Physical Review Letters (2012) is fundamentally flawed in its interpretation as discussed by Berengut and Flambuam.

    III. The Fine-tuning Problem

    Understanding the universe
      For a discussion of this issue we refer to a Paper by Hogan, entitled: 'Why the Universe is just so'. A Basic issue is that our Universe is special in the sense that it allows for complexity.

    What is Fine tuning
      We live in a Universe in which a certain high level of complexity is produced. This complexity is dependent on the fact that multiple elements have been produced (over a hundred), that atoms and molecules can be bound, and that the time scale of the Universe is sufficiently long so that stars, galaxies, and black holes could form.

      In the picture it is shown that a Universe may develop into one where matters rapidly diverges so that galaxy formation will not occue, or the opposite of leading to a rapid big crunch. Our Universe is tuned into one of a 'long time scale' where all these processes giving rise to complexity occur. One of the characteristics of our Universe is that some 1017 black holes exist, instead of the intuitively more likely 0 (rapid expansion) or 1 (immediate big crunch).

    Example: the Hoyle resonance
      A celebrated example of a fine-tuned process is that of the production of carbon and oxygen elements occurring in the final stages of stars (super-nova explosions), in which all heavy elements (heavier than Li) existing in the universe have been formed. There is a nuclear process, where a resonant energy level plays a decisive role.
      Carbon and oxygen are produced by the following sequence of nuclear reactions:
        4He + 4He --> 8Be
        4He + 8Be --> 12C
        4He + 12C --> 16O
      Since the first reaction proceeds rapidly it was realized that the second reaction must be enhanced through a resonance in the level energy scheme of carbon-12. After Hoyle had proposed that such a resonance must lie at 7.65 MeV it was measured to fall at 7.656 MeV, as predicted. Another requirement for the He-Be-C-O cycle to proceed is that the (unstable) Be-8 nucleus has a sufficiently long lifetime. Moreover the 3rd reaction is not resonant: the reaction energy of He-4 and C-12 is 7.16 MeV while the O-16 nucleus has 7.11 MeV, hence the reaction is allowed but not resonant. The level structure of quantum states in nuclei critically and sensitively depends on the strength of the nuclear (strong) force and the electromagnetic force. Small variations in the coupling constants (fundamental constants) will cause the level structure to change. Hence the exact position of the resonance in the 2nd reaction (the Hoyle resonance) depends sensitively on the values of LamdaQCD and alphaEM. This is shown in the figure below. This topic has been worked out in detail in the Paper by Oberhummer et al.

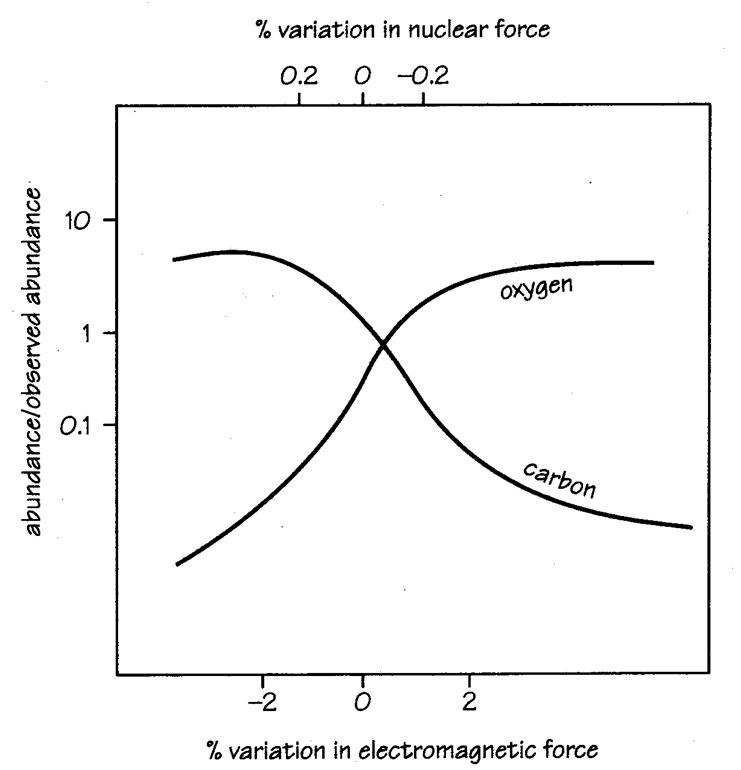
        Graph of the Hoyle resonance; production of C and O as a function of the fundamental constants.

    The Anthropic Principle
      It is not surprising with these fortuitous values adopted by the fundamental constants, that this has become the subject of speculation, often in terms of a 'designer' or in terms of an 'anthropic principle'. A key pulication on the anthropic principle is that of Carr and Rees on The anthropic principle and the structure of the world. The proposal of the Anthropic Principle is ascribed to Brandon Carter in 1973.
      This topic is also the subject of a book by:

        by Barrow and Tipler.

    Cosmological Natural Selection

    IV. Constraining Fundamental Constants

    Observational quantities as measured for various stages of the development of the Universe can be confronted with theoretical models to derive values (and their time-variance) for the fundamental constants for a particular epoch. For a short review of the various methods we refer to the Paper by Webb.

    Big Bang Nuclear Synthesis
      Models have been devised for the evolution of the Universe in the first few minutes in which the light elements are produced. The reactive processes (of nuclear fusion) have a certain outcome, in particular resulting in the relative distribution of elements over H, D, 3-He, 4-He and 7-Li. The nuclear reactions are determined by the strength of the strong force (Lambda_QCD) and the weak force. The latter comes in because the lifetime of the neutron (decaying within some 11 minutes due to beta-decay, hence the strength of the weak force) is a crucial factor. The strong force determines the (small) binding energy of the deuteron, and therewith the temperature at which deuterium can withstand photo-desintegration.

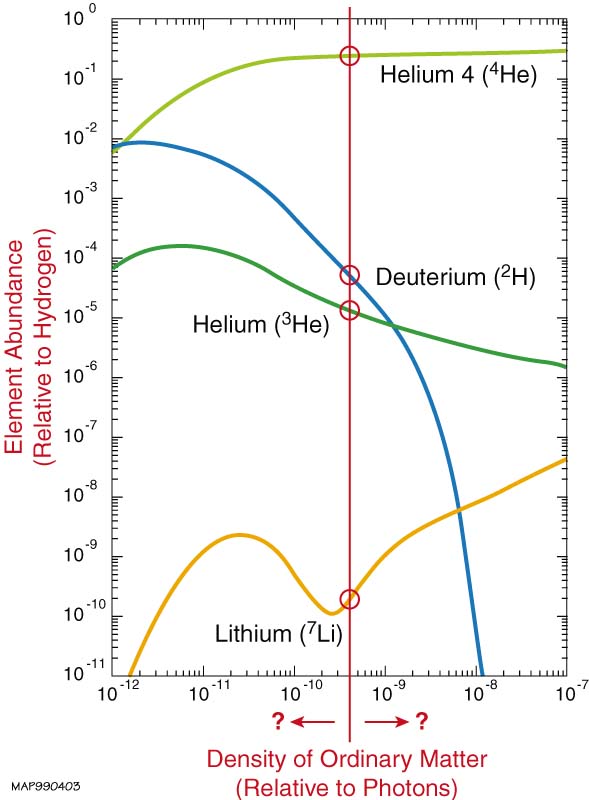
        Models of Big Bang nuclear synthesis of elements as a function of the ratio photons/baryons, matched to a certain distribution of elements.
      A review of BBN is given in the following review paper: Primordial nucleosynthesis: theory and observations.

    The OKLO phenomenon
      A French engineer found that the 235-U/238-U ratio in an uranium mine in Gabon was off from the Earth-average value by a small percentage. From this and other facts it was concluded that this mine had operated as a natural nuclear energy reactor some 2.5 Gyr ago. From the ratio of abundancies of other elements (Samarium and Neodymium) a value for the strength of the nuclear force and the fine-structure constant (at the time of operation) were derived, taking into account some resonances in the nuclear structure of some nuclei. This delivers a constraint on the time variation of both alpha and Lambda_QCD. In view of the fact that these analyses are difficult, and a number of assumptions have to be made, various reanalyses have been made over the years leading to differing results. The issue is still under debate and a general description is given in the Paper by Webb.

    The Alkali-Doublet method
      As is well-known from elementary atomic physics the spectral splitting in two components of the S-P transitions in alkali atoms is related to the fine structure constant (in fact alpha-square); the fine structrue constant is named after this 'fine-structure' splitting. One example is the splitting of the Na-D line at 589 nm; such doublet splittings also occur in some ionized atoms: Si II or O III. Such spectral splittings can be used to determine the value of alpha, and this was a first handle to search for alpha-variation. Alkali-doublet features can be observed in the emission spectra of quasar sources, and later also in the absorption spectra of cold absorbing clouds in the foreground of quasar sources. The (cosmological) time scale of the emissions/absorptions can be deduced from the red-shift of the objects. Bahcall and Schmidt were the one to derive tight constraints from quasar spectra based on this alkali-doublet method. See their paper: Does the fine-structure constant vary with cosmic time ?.

    The Many Multiplet method
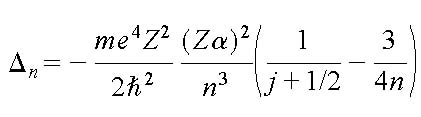
      The energy levels in atoms scale according to the Rydberg formula, where the energy scale is the Rydberg (proportional to the hartree, the atomic unit). In the non-relativistic limit all atomic spectra are proportional to the Rydberg constant, and can therefore not be used to detect a variation in alpha; such effect would be absorbed by the redshift parameter z. Relativistic corrections to the levels however do depend on the fine structure constant alpha:

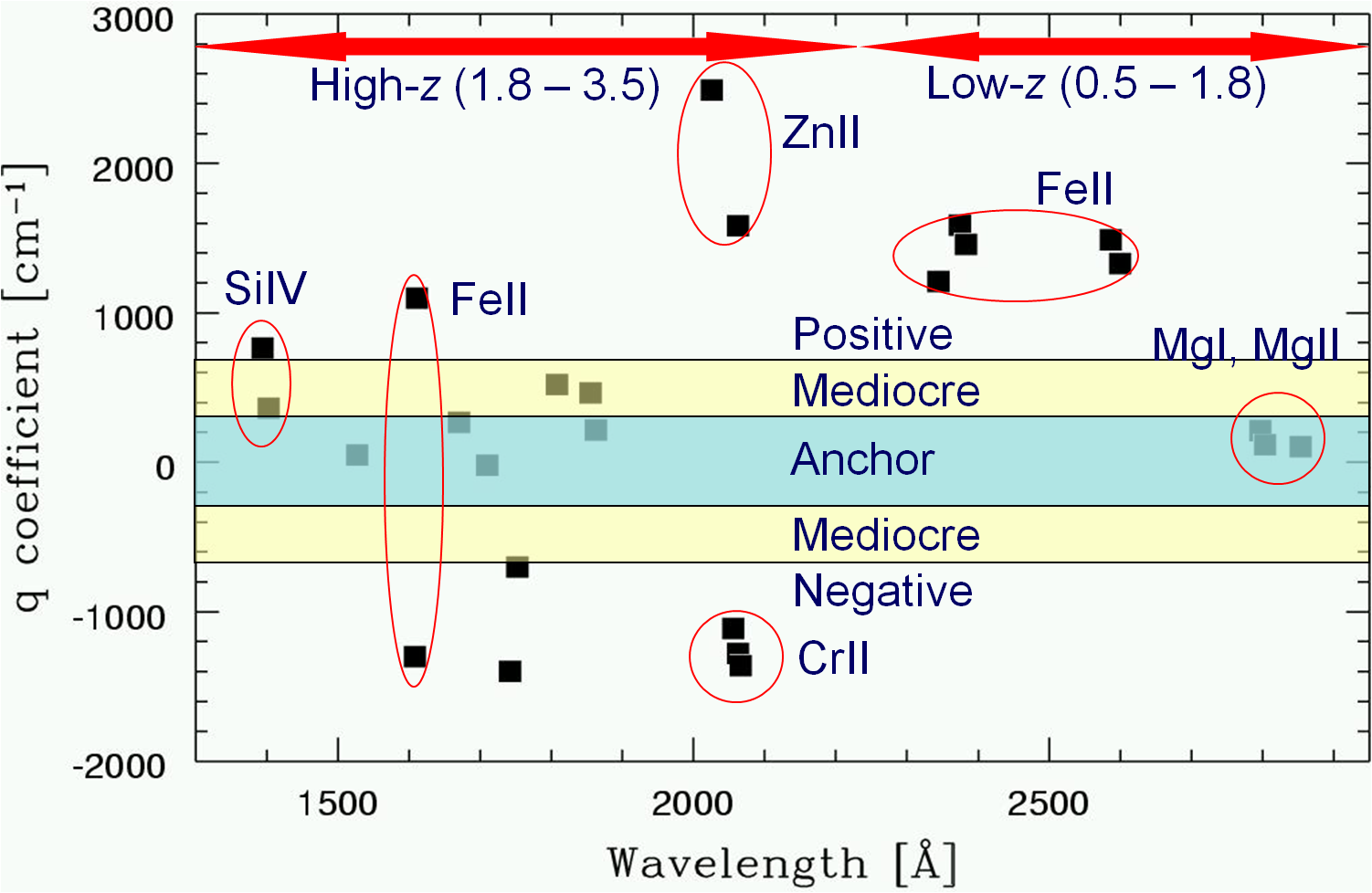
      This causes the transition frequencies to depend on the fine structure constant, and this effect is enhanced by many-body effects and scales with Z2. The sensitivity of a certain transition to a variation of alpha (expressed by a coefficient q) therefore depends on the specific atom (and its Z). It also depends on the electronic orbital configuration. Because of these phenomena the transition frequencies of multiple atoms (ions) can be used to deduce an effect of a varying alpha, hence this method is dubbed the: Many-Multiplet method, as described by Dzuba, Flambaum and Webb.

        Figure (cf. M.T. Murphy) representing the q-sensitivity coefficients of the various atomic lines; note the positive shifters, negative shifters and anchor lines.

    Laboratory experiments on alpha-variation
      By now a great number of laboratory experiments have been performed that lay a firm constraint (upper limit) to a possblie variation of the fine structure constant. Such studies probe varaying constants in the modern epoch and cover time intervals of a few years only, hence they require extremely precise frequency measurements. The experiments are performed with modern optical clocks, either based on neutral atoms confined in optical lattices, or on charged ions confined in ion traps. A number of experiments are reviewed by Peik (2010) in his paper on: Fundamental constants and units.
      The advantage of laboratory experiments is that the objects of study can be chosen for their sensitivities. In some atoms, not present in outer space, accidental resonances occur exhibiting extremely large sensitivity coefficients. A specific example is that of a resonance between excited levels in the Dysprosium atom (see Paper-1, Paper-2), which has been subject to a study searching for a varying alpha on a laboratory time scale.
      As for mu-variation not many laboratory experiments have been performed. An important constraint has been produced by Chardonnet and coworkers measuring narrow transitions in te SF6 molecule. See: Paper on SF6.

    The sensitive 229-Th clock
      Optical transitions in the quantummechanical level scheme of a nucleus sometimes can occur due to a fortunate ordering of quantum states. In the nucleus of 229-thorium such a phenomenon is known to exist at 7.5 eV. (See paper: Peik and Tamm 2003). Calculations have been performed on the level energies of the 229-th nucleus and it was shown that the sensitivity for a variation of alpha, as well as a variation of the coupling constant for the nuclear force (proportional to mu) is ver large (See paper: Flambaum 2006). Of course it is difficult to perform spectroscopy on a nucleus in particular since the nucleus is shielded from the optical radiation by the electron cloud around the molecule. A technique of "bridging spectroscopy" is proposed as a way out (See paper: Porsev et al. 2010).

    V. Molecular Physics

    Variation of the proton-electron mass ratio is often studied in molecules, since the spectra of atoms only marginally depend on this constant. Therefore it is needed to acquire understanding of the level structure of molecules.

    The level structure of diatomic molecules
      Diatomic molecules are the simplest molecules with only a limited number of degrees of freedom. They serve as exemplary to study the level structure of molecules, starting from the Schroedinger equation, the Born-Oppenheimer approximation, the separation of nuclear and electronic degrees of freedom, the harmonic oscillator description of vibrations and the quantum-mechanical angular momentum description of rotational motion. For these topics study the: Lecture notes on diatomic molecules. The notes also contain a chapter on open shell molecules, or radicals, which will be discussed.

    The calculation of sensitivity coefficients Ki for mu-variation
      Each spectral line in a molecular spectrum is sensitive in a different way to a possible variation of the proton-electron mass ratio, in the same way as each line undergoes a different isotope shift. Such sensitivities can be expressed as:
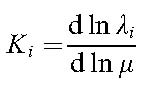        or in terms of frequency
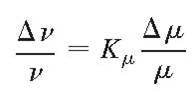
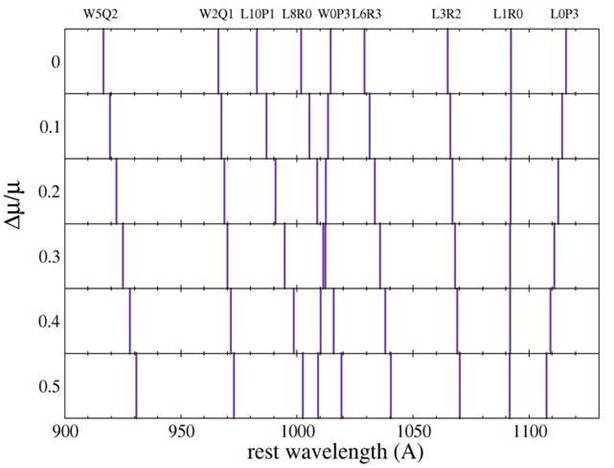
      The sensitivity coefficients Ki can be calculated from molecular structure theory, either by quantum ab initio calculations or by semi-empirical approaches. Even quick estimates can be made based on the Born-Oppenheimer approximation, where the energy of each lines is divided into an electronic, vibrational and rotational contribution. Then one may impose that electronic energies do not (only marginally) depend on mu, vibrational energies scale as the square-root (harmonic oscillator) and rotational contributions scale linearly with mu (moment of inertia). The figure below shows some lines in the spectrum of H2 shifting towards the red and blue, whereas other lines act as anchor lines.

        Figure displaying the response of H2 spectral lines to a variation of the proton-electron mass ratio
      A full account fo the calculation of sensitivity coefficients in H2 and methods of analysis of H2 in quasar spectra is given in the following Paper.

    Resonances in Ki
      Sensitivity coefficients can be calculated for levels as well as for transitions. Special cases may occur where energy levels come into close resonance; this is accompanied by a shift of the transition frequency into the long-wavelength or low-frequency regime. As may be seen from the equations expressing the K-coefficient for transitions and energy levels:
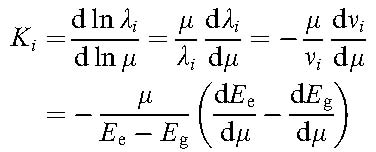
      the K-coefficient may be resonantly enhanced in cases of near-degeneracy, in particular if the quantum numbers associated with the two near-resonant levels are strongly different. This may happen if one level is electronically excited, while the other is vibrationally excited, or any other combination. Resonance in Ki occurs if both levels exhibits a strongly different dependence on mu. Many of such resonances exist: Atomic dysprosium was proposed as a sensitive test system to detect a variation of alpha on a laboratory time scale. Also various examples of resonance behaviour are discussed in the literature, see e.g. Bethlem. In the example of methanol, discussed below, resonances play a role as well.

    VI. Analysis of quasar spectra

    Modern very large telescopes can be used to record high-resolution spectra of quasi-stellar objects or quasars. Note that the light from the very bright quasar objects is used as a background light source and that absorption spectra of the cold environment of gases clouds in the interstellar medium pertaining to foreground galaxies, located at redshifts in the range z = 0.5 -4, is measured. From these spectra estimates are made on a possible variation of fundamental constants on a cosmological time scale. Cosmological models relate the observed redshift z to look-back times.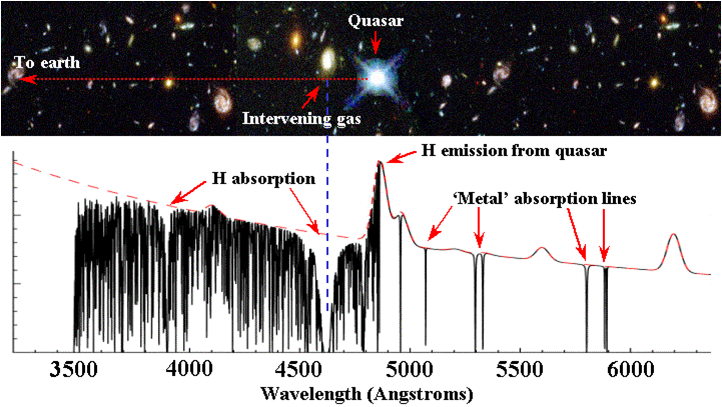

      A typical quasar spectrum in the optical range with a damped-Lyman-alpha system in the path; note the "Lyman-alpha forest".

    alpha-variation from analysis of metal spectra
      Possible variation of alpha on a cosmological time scales is derived from comparison of spectroscopic lines of metal (astronomers consider metals anything but hydrogen and helium). Fortunately several important metal lines (Mg-ion and Fe-ion are important) lie in the range redward of the Lyman-alpha emission peak and the Lyman-alpha forest.

    mu-variation from analysis of H2 spectra
      Damped-Lyman-alpha absorption systems (high-redshift absorbing clouds with hydrogen column densities (H I) larger then 1020 per cm2 usually exhibit detectable amounts of molecular hydrogen with often many strong lines in the Lyman and Werner band systems of H2. These lines all have different Ki coefficients and form the basis to search for a varying mu at cosmological distance. Such spectra are difficult to analyze because of the overlapping Lyman-alpha-forest. For an extensive description see: Malec et al.

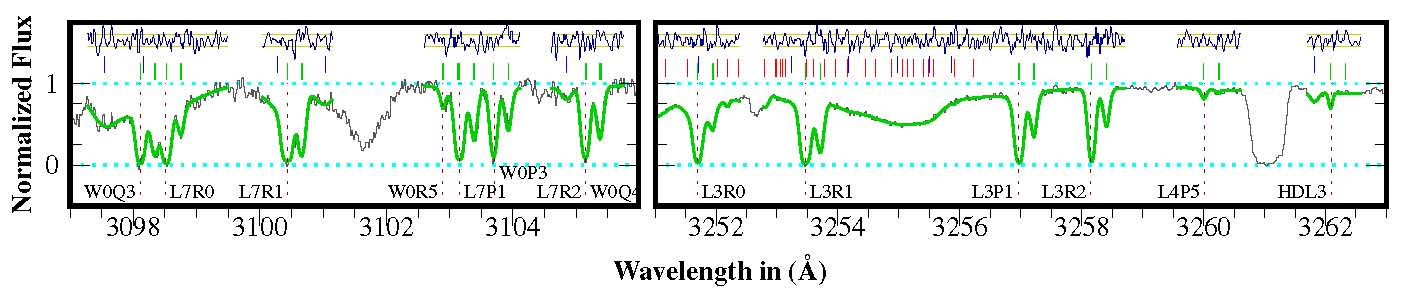
        A typical (portion of a) H2 absorption spectrum twoard the J2123 quasar; the absorbing cloud is at z = 2.05.

    Radio-astronomical detection of molecules; the case of ammonia
      One may consider what molecules, and what degrees of freedom, may give rise to sensitive transitions in molecular spectra, or transitions with a high sensitivity coefficient. It is known form basic quantum mechanics that tunneling motions are exponentially dependent on the mass of the tunneling particle; in the ammonia molecule (NH3) there exists a degree of freedom whereby the N-atom tunnels through the plane of the three H-atoms. This inversion splitting has been investigated since the blossoming period of microwave spectroscopy (Shawlow and Townes 1950s); in fact this inversion spectral line was detected as the first maser line in the laboratory and was eraly on suggested as the carrier of an atomic clock resonance. The inversion frequency has a large isotope shift and a large sensitivity coefficient (K=-4.2 for NH3), as calculated in the paper by Flambaum and Kozlov; see also the figure below:

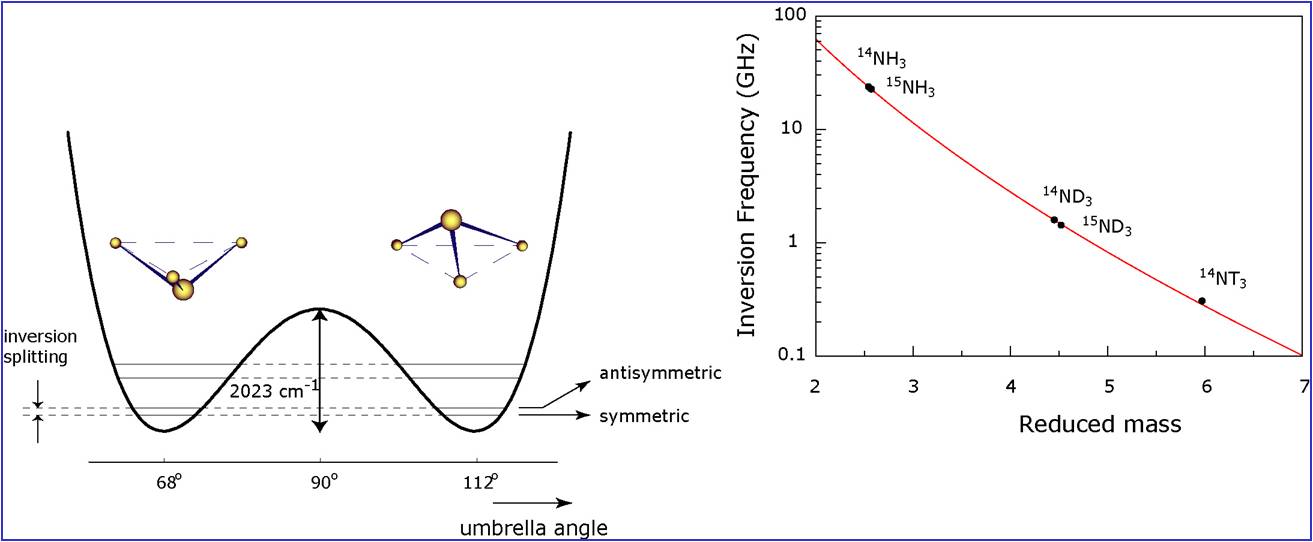
        The inversion tunneling motion in ammonia and the high sensitivity of the tunneling frequency.

      This extreme sensitivity of the ammonia molecule for a variation of the proton-electron mass ratio was used to derive an upper limit to a variation from the radio-source B0218+357 at redshift z=0.68466 in the paper by Murphy et al..

      Radio-astronomical detection of molecules; the improved case of methanol
        Recently it was found that hindered rotation in molecules such as methanol (in fact also a quantum tunneling process) can give rise to even higher sensitivity coefficients, up to K=40. See the: Methanol paper. This strong effect is also related to some cancellation of contributions to the total energy in the molecule: overall rotational energy is "converted" into tunneling (or torsional) energy; this is in fact a resonance effect. Note that the molecular level structure of molecules as methanol is rather complex, since the molecule may rotate around three external axes, as well as around an internal axis. The spectral lines of both ammonia and of methanol fall in the microwave regime, since no electronic or vibrational motion is excited. Such lines can be detected in radio-astronomy. In fact very recently four lines of methanol were observed with the Effelsberg radio telescope toward the system PKS-1830-211 at redshift z=0.89, leading to a constraint of Dm/m < 10-7. See the story on Molecular matter has not changed in the past 7 billion years.
        Since the first observations of methanol with the Effelsberg telescope methanol lines have been observed at other radio telescopes, probing also higher frequencies, like on the IRAM and ALMA observatories. This has led to an analysis of mu-variation based on data from three radio telescopes: Methanol at three radio telescopes.
        Unfortunately there is only a single object at high redshift where methanol is observed: PKS-1830-211 at redshift z=0.89. This limits the detection of mu-variation.

      Status on mu-variation on a cosmological time scale
        Various studies on spectra of molecules detected at high redshift have been performed in the past decade. Ammonia is observed for z < 1, by radio astronomy with the farthest distant object found at z =0.89. Hydrogen molecules can be observed for z >2 in view of atmospheric transparancy. Constraints on mu-variation are displayed in the graph below. Note that ammonia is more sensitive than H2.

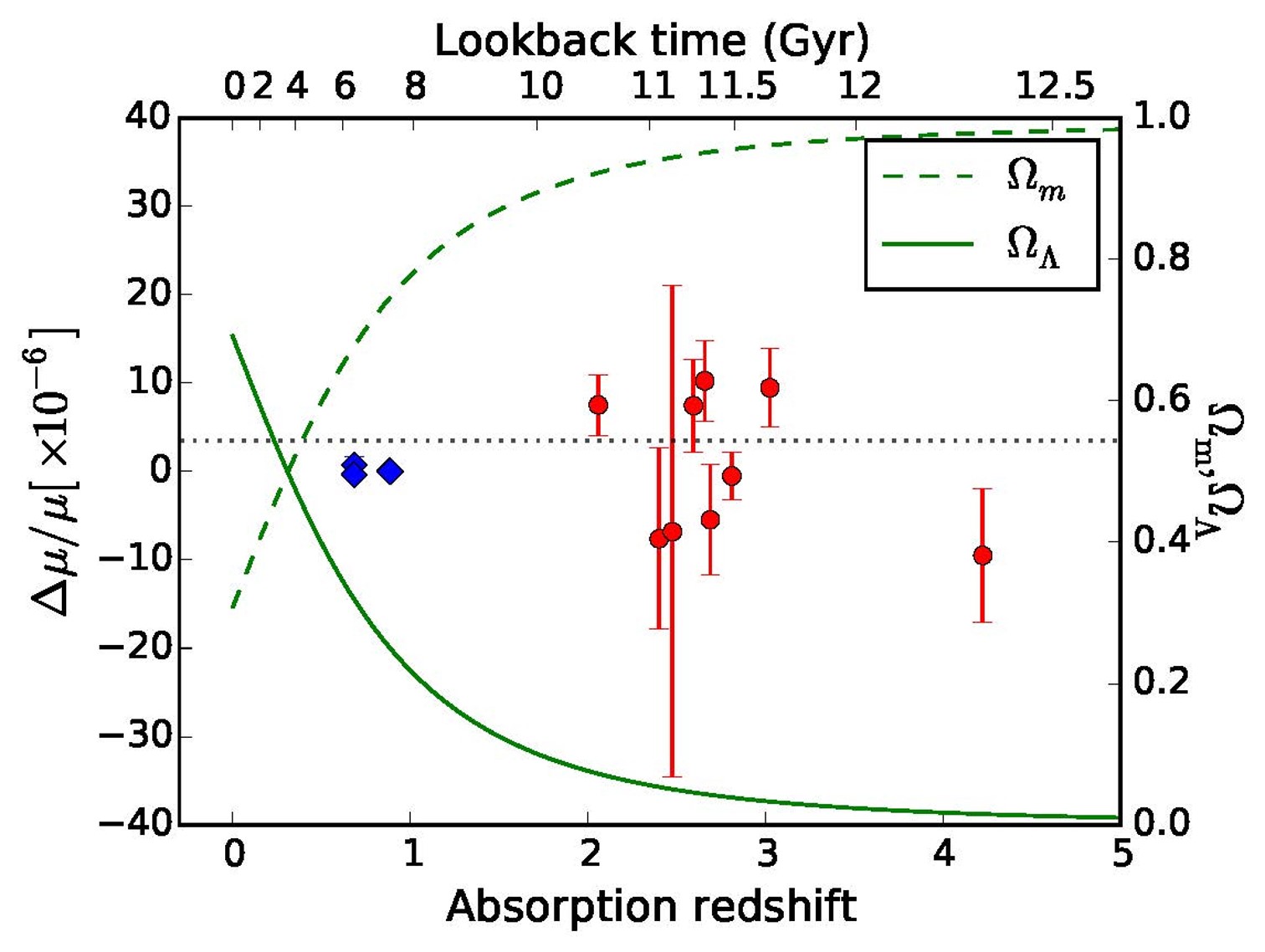
        Current status of mu-variation analyses; for a discussion see the paper: Review paper. The blue points refer to the measurements on ammonia and methanol, providing much tighter constraints - beacuse of the larger sensitivity of those species.
        Thusfar 10 quasar absorption systems have been observed (9 displayed) at high resolution and a varying constant analysis performed. The overall result can be phrased as: the proton-electron mass ratio (mu) has changed by less than 5 ppm in the interval z=2-4.2, or for look-back times of 10-12.5 Gyrs.
        Note the plotted graphs for the historic evolution of the matter content in the Universe (dashed) and the dark energy content (full line). No proportionality with dark energy is found. This means that there is no such connection, or the level of detection is not sufficiently sensitive.

      Mu-variation in gravitational fields
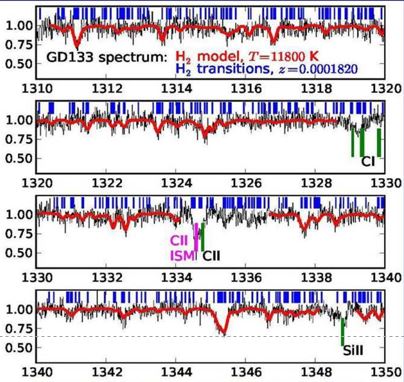
        This is an entirely different subject. General relativity predicts that the laws of physics should not depend on a specific location, hence not on the magnitude of a gravitational field. This law can be tested by measuring the value of a fundamental constant for varying gravitational fields. One posibility is to employ the ellepticity of the Earth orbit around the sun; another is to employ molecules in the strong field in white dwarfs exhibiting a gravitational potential much larger than at Earth (typically 10000 times larger). Spectra of hydrogen molecules in the hot photospheres (typically 10000 K) of white dwarfs can be analyzed. For such analyses the dim spectra of white dwarfs in our Milky Way galaxy are used, meaning that there is no redshift and the spectra are in the vacuum ultraviolet. Typically such observations were done with the Hubble Space Telescope.
          ......
        The result of an analysis of H2 in the photosphere of GD133 yields a constraint on the variation in the value of mu of less than 50 ppm. This is described in: Paper White Dwarfs.