In het Compton effect worden ![]() -ray fotonen (zogenaamde
Röntgenstralen) over een hoek
-ray fotonen (zogenaamde
Röntgenstralen) over een hoek ![]() verstrooid aan vrije
elektronen. Hierdoor zal de golflengte van de fotonen toenemen
met het bedrag
verstrooid aan vrije
elektronen. Hierdoor zal de golflengte van de fotonen toenemen
met het bedrag
![]() .
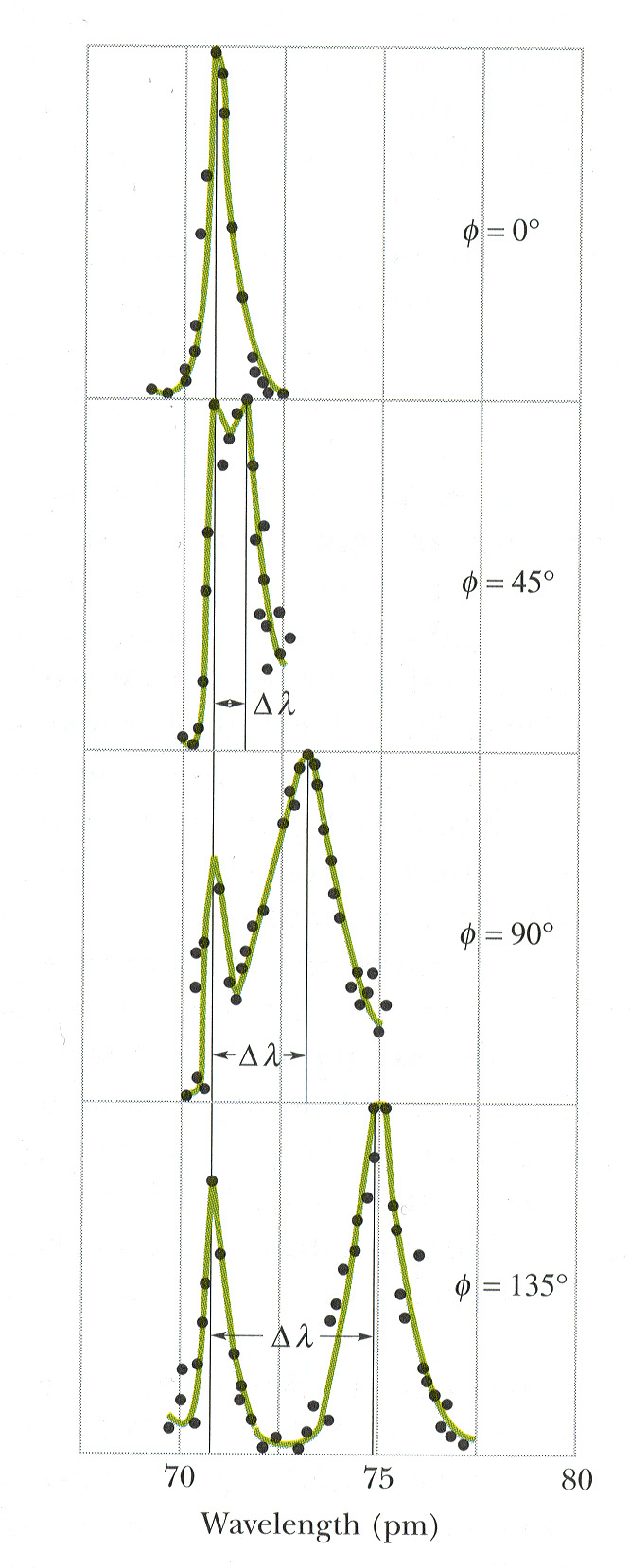
Deze Compton verschuiving wordt gegeven door
.
Deze Compton verschuiving wordt gegeven door
| (7) |
We kunnen de uitdrukking voor
![]() afleiden door
energie- en impulsbehoud te combineren. Voor energiebehoud geldt
afleiden door
energie- en impulsbehoud te combineren. Voor energiebehoud geldt
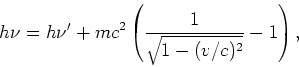 |
(8) |
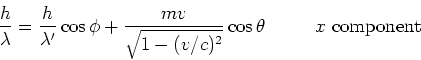 |
(9) |
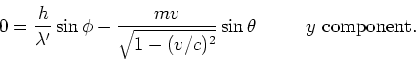 |
(10) |
Merk op dat zowel in de vergelijking van het fotoelektrisch effect
en het Compton effect de constante van Planck voorkomt. Deze
constante, alhoewel klein, is het bepalende kenmerk van de moderne
quantummechanica. De studie van de golflengteverdeling van de
straling die uitgezonden wordt door verwarmde zwarte lichamen,
gaf als eerste aanleiding tot het concept van energie quantisatie,
en hiermee werd de constante van Planck in de moderne fysica
geïntroduceerd.