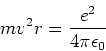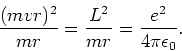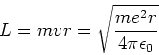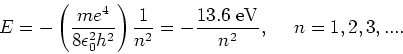Next: LES 02
Up: INLEIDING
Previous: Compton Effect
De absorptie en emissie van straling bij scherp gedefinieerde
golflengten is karakteristiek voor atomen, moleculen en kernen.
De representaties van deze golflengten worden lijnenspectra
genoemd. Enkele van de energieniveaus van het waterstofatoom
worden gegeven in Fig. 4.
De klassieke fysica heeft geen verklaring voor deze fenomenen.
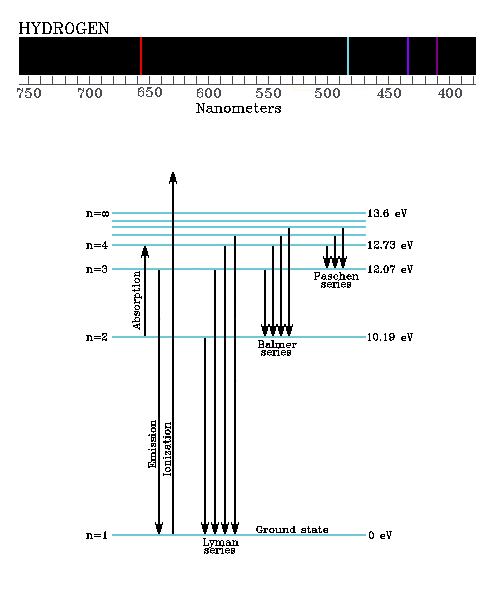 Figure 4:
Enkele van de belangrijkste energieniveaus en
transities voor het waterstofatoom.
Figure 4:
Enkele van de belangrijkste energieniveaus en
transities voor het waterstofatoom.
De pogingen om de lijnenspectra te beschrijven beginnen bij
de quantum postulaten van Niels Bohr. Hij trachtte als
eerste het spectrum van waterstofatomen te verklaren door
aan te nemen dat
Het atoommodel dat aan het begin van de eeuw werd ontwikkeld, was
gebaseerd op metingen van de Engelse fysicus Ernest Rutherford.
Hierbij kan men bijvoorbeeld een waterstofatoom vereenvoudigd voorstellen
als een elektron dat in een cirkelvormige baan
beweegt rond de kern gevormd door een proton.
Een en ander is weergegeven in Fig. 5.
 Figure 5:
Een klassiek model van het waterstofatoom, waarbij een
elektron met massa
Figure 5:
Een klassiek model van het waterstofatoom, waarbij een
elektron met massa 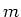 een cirkelvormige beweging uitvoert rond
een centrale kern met massa
een cirkelvormige beweging uitvoert rond
een centrale kern met massa 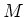 . We nemen aan dat
. We nemen aan dat 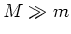 .
.
In het volgende geven we een eenvoudige afleiding (suggestie van Niels
Bohr) van de formule voor de energieën van de stationaire toestanden.
We passen de tweede wet van Newton, 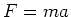 , toe op het ronddraaiende
elektron en gebruiken de wet van Coulomb om de kracht op het elektron
te vinden. Er geldt
, toe op het ronddraaiende
elektron en gebruiken de wet van Coulomb om de kracht op het elektron
te vinden. Er geldt
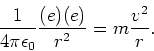 |
(12) |
Voor de kinetische energie van het elektron vinden we
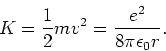 |
(13) |
De elektrische potentiële energie van het elektron-proton
systeem is
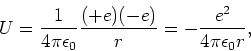 |
(14) |
en de totale energie van het atoom is
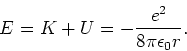 |
(15) |
We hebben dus nu een uitdrukking voor de energie van het waterstofatoom
afgeleid gebruikmakend van zuiver klassieke wetten. De totale energie
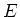 van iedere stationaire toestand hangt af van de straal van de
baan die hoort bij die toestand. Als we nu niet een uitdrukking voor
deze stralen vinden, dan zitten we klem. Kortom, we hebben een quantisatie
criterium nodig teneinde discrete energiespectra te vinden.
van iedere stationaire toestand hangt af van de straal van de
baan die hoort bij die toestand. Als we nu niet een uitdrukking voor
deze stralen vinden, dan zitten we klem. Kortom, we hebben een quantisatie
criterium nodig teneinde discrete energiespectra te vinden.
Om de energieën van de stationaire toestanden in waterstofatomen
te vinden heeft Bohr aangenomen dat het baanimpulsmoment 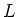 van een circulerend elektron enkel discrete waarden kan aannemen
die gegeven worden door
van een circulerend elektron enkel discrete waarden kan aannemen
die gegeven worden door
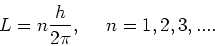 |
(16) |
Merk op dat impulsmoment en de constante van Planck dezelfde
eenheid hebben. Wellicht maakt dit feit het wat minder verrassend
dat impulsmoment ons de meest eenvoudige quantisatieregel geeft.
We weten dat 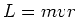 en kunnen met behulp van vergelijking (12)
schrijven dat
en kunnen met behulp van vergelijking (12)
schrijven dat
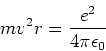 |
(17) |
en vinden dan
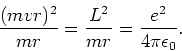 |
(18) |
We vinden voor het baanimpulsmoment
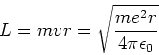 |
(19) |
en hierbij volgt voor de stralen van de mogelijke toestanden
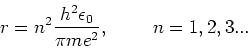 |
(20) |
De resulterende energieën voor de toegestane toestanden kunnen
nu eenvoudig gevonden worden. Er volgt
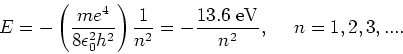 |
(21) |
Hierbij is 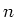 een zogenaamd quantumgetal.
een zogenaamd quantumgetal.
Indien we de frequentieconditie met bovenstaande uitdrukking combineren,
dan vinden we
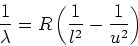 |
(22) |
voor de golflengten tussen de lijnen van het waterstofspectrum voor een
transitie van een hogere (upper) toestand met quantumgetal 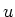 naar
een lagere (lower) toestand met quantumgetal
naar
een lagere (lower) toestand met quantumgetal 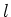 . Hierbij is
. Hierbij is
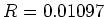 nm
nm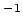 de zogenaamde Rydberg constante.
de zogenaamde Rydberg constante.
Het blijkt dat dit relatief eenvoudig formalisme in verrassend goede
overeenstemming (beter dan 0.02 % voor het waterstofatoom)
is met de gemeten spectra. De postulaten van Niels Bohr vormden
een deel van de basis van de quantummechanica.



Next: LES 02
Up: INLEIDING
Previous: Compton Effect
Jo van den Brand
2000-10-21



![]() , toe op het ronddraaiende
elektron en gebruiken de wet van Coulomb om de kracht op het elektron
te vinden. Er geldt
, toe op het ronddraaiende
elektron en gebruiken de wet van Coulomb om de kracht op het elektron
te vinden. Er geldt
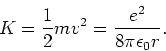
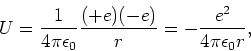
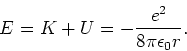
![]() van een circulerend elektron enkel discrete waarden kan aannemen
die gegeven worden door
van een circulerend elektron enkel discrete waarden kan aannemen
die gegeven worden door
![]() en kunnen met behulp van vergelijking (12)
schrijven dat
en kunnen met behulp van vergelijking (12)
schrijven dat