


Next: Oneindige Rechthoekige Put Potentiaal
Up: Een-Dimensionale Oplossingen van de
Previous: Stap Potentiaal met
We nemen weer aan dat een vrij deeltje zich beweegt in de richting van
een constante potentiaal,
 voor
voor 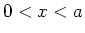 .
De situatie is geschetst in Fig. 16.
.
De situatie is geschetst in Fig. 16.
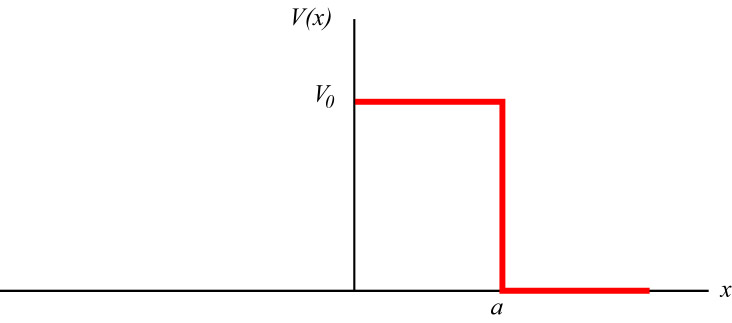 Figure 16:
Schematische voorstelling van een vrij deeltje
dat onderhevig is aan het tunnel effect.
Figure 16:
Schematische voorstelling van een vrij deeltje
dat onderhevig is aan het tunnel effect.
We onderscheiden nu drie gebieden.
We merken op dat er in het gebied rechts van de barrière enkel een
doorgelaten golf kan bestaan en dus stellen we 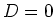 .
.
In onze analyse beschouwen we nu eerst het geval dat
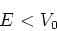 |
(163) |
is. De toestandsffunctie en zijn eerste afgeleide dienen weer eindig en
continue te zijn op de punten 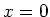 en
en 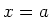 . Hierdoor krijgen we vier
vergelijkingen met de willekeurige constanten
. Hierdoor krijgen we vier
vergelijkingen met de willekeurige constanten 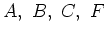 en
en 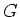 . Deze
vergelijkingen kunnen gebruikt worden om
. Deze
vergelijkingen kunnen gebruikt worden om 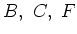 en
en 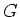 uit te drukken
in
uit te drukken
in 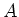 . De waarde van
. De waarde van 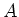 kan dan weer in principe uit de normering
bepaald worden. De waarschijnlijkheidsdichtheid is schematisch weergegeven
in Fig. 17.
kan dan weer in principe uit de normering
bepaald worden. De waarschijnlijkheidsdichtheid is schematisch weergegeven
in Fig. 17.
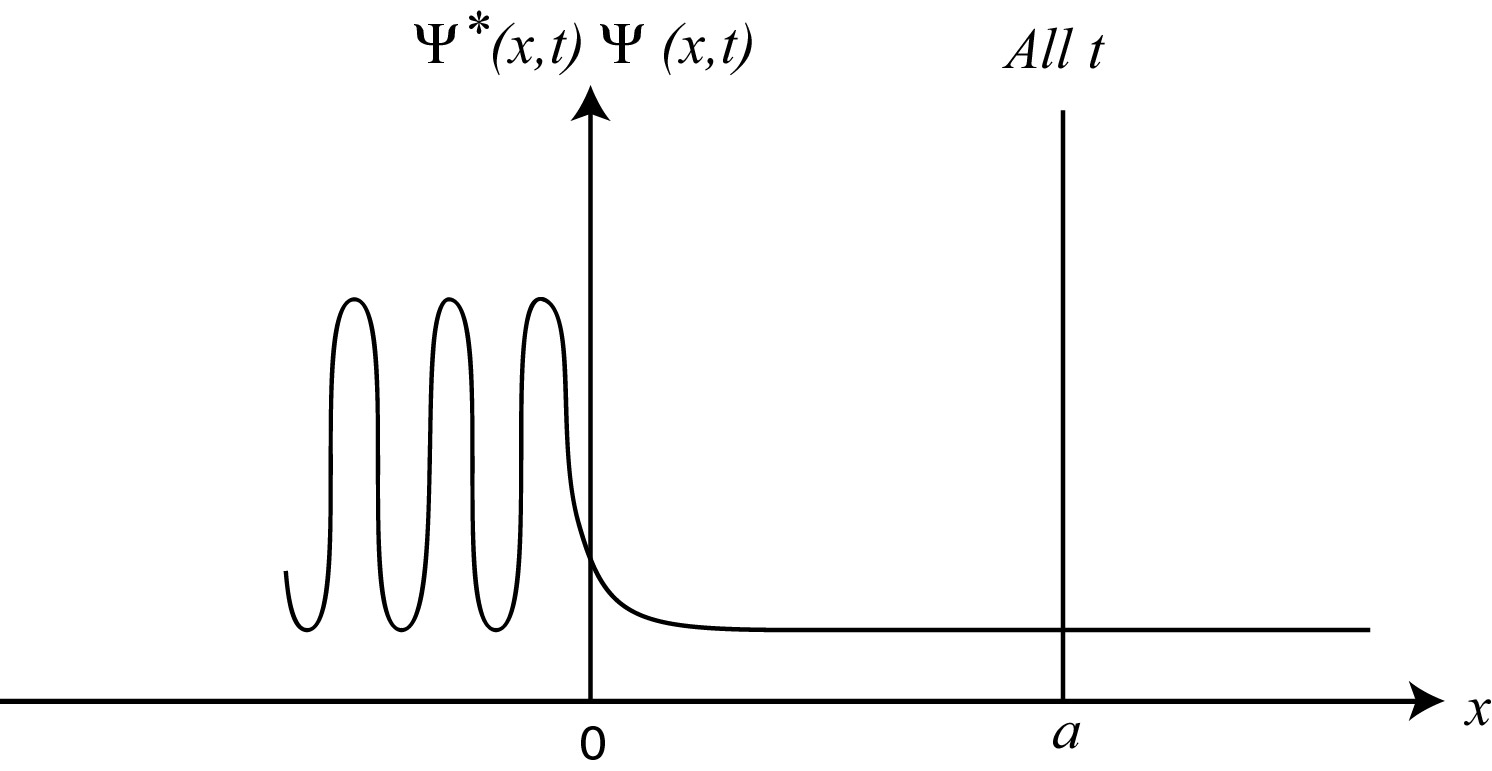 Figure 17:
Typische verdeling van de waarschijnlijkheidsdichtheid
Figure 17:
Typische verdeling van de waarschijnlijkheidsdichtheid
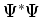 voor een situatie met tunnel effect.
voor een situatie met tunnel effect.
In het gebied 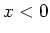 is de golffunctie grotendeels een staande golf,
maar bevat een kleine bijdrage van een lopende golf, omdat de
gereflecteerde golf een kleinere amplitude heeft dan de inkomende golf.
In het gebied
is de golffunctie grotendeels een staande golf,
maar bevat een kleine bijdrage van een lopende golf, omdat de
gereflecteerde golf een kleinere amplitude heeft dan de inkomende golf.
In het gebied 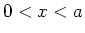 is de golffunctie een staande golf
waarvan de amplitude exponentieel afneemt. Het meest interessant is
het de coëfficiënt
is de golffunctie een staande golf
waarvan de amplitude exponentieel afneemt. Het meest interessant is
het de coëfficiënt 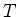 uit te rekenen, die de verhouding geeft
van de doorgelaten waarschijnlijkheidsflux in het gebied
uit te rekenen, die de verhouding geeft
van de doorgelaten waarschijnlijkheidsflux in het gebied 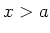 ten opzichte van de inkomende flux. Een berekening geeft
ten opzichte van de inkomende flux. Een berekening geeft
![\begin{displaymath}
T={v_1{\mathcal{C}}^*{\mathcal{C}} \over v_1 {\mathcal{A}}^*...
...E \over V_0}
\left( 1- {E \over V_0} \right) } \right]^{-1} ,
\end{displaymath}](img450.gif) |
(164) |
waarbij
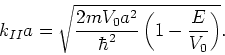 |
(165) |
Voor gevallen waarbij de exponent erg groot is simplificeert de
vergelijking tot
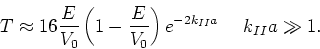 |
(166) |
Deze vergelijkingen geven een voorspelling van een opmerkelijk feit
(gezien vanuit het gezichtpunt van de klassieke mechanica) dat een
deeltje met massa 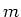 en energie
en energie 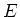 , dat invalt op een barrière
met hoogte
, dat invalt op een barrière
met hoogte 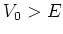 en eindige dikte
en eindige dikte 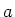 , een zekere waarschijnlijkheid
, een zekere waarschijnlijkheid
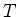 heeft om deze barrière te penetreren. Dit verschijnsel heet
het tunnel effect.
heeft om deze barrière te penetreren. Dit verschijnsel heet
het tunnel effect.
We beschouwen vervolgens het geval dat
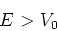 |
(167) |
is.
We vinden nu voor de transmissiecoëfficiënt 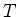
![\begin{displaymath}
T={v_1{\mathcal{C}}^*{\mathcal{C}} \over v_1 {\mathcal{A}}^*...
...E \over V_0}
\left( {E \over V_0} -1 \right) } \right]^{-1} ,
\end{displaymath}](img455.gif) |
(168) |
waarbij
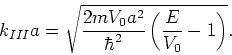 |
(169) |
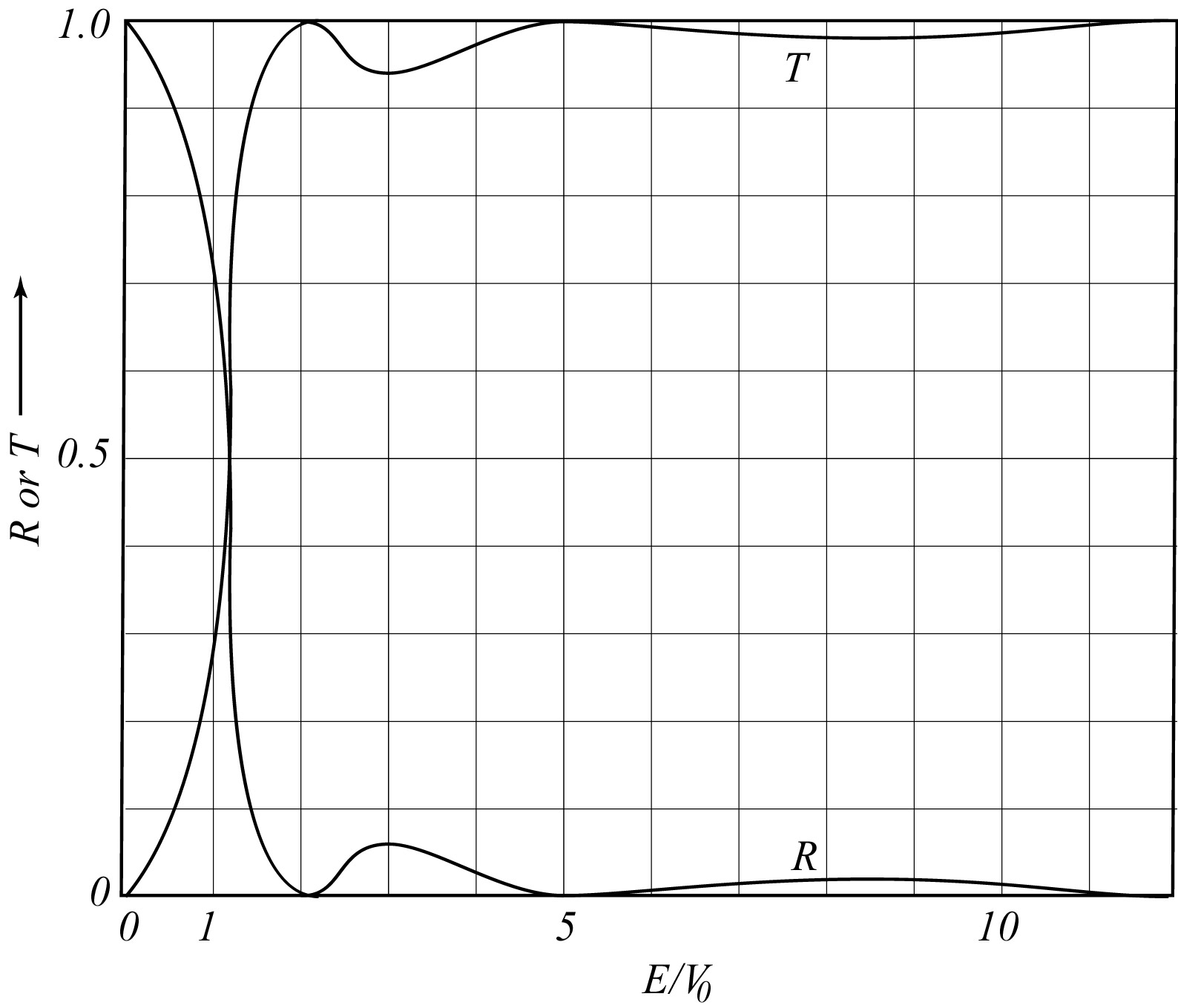 Figure 18:
Reflectie en transmissiecoëfficienten
Figure 18:
Reflectie en transmissiecoëfficienten 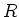 en
en 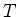 voor
een deeltje dat verstrooit aan een barrière met hoogte
voor
een deeltje dat verstrooit aan een barrière met hoogte 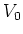 en dikte
en dikte 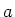 ,
zodanig dat
,
zodanig dat
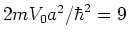 .
.
Fig. 18 toont 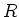 en
en 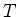 voor een deeltje dat aan een
stap potentiaal verstrooid. Merk op dat
voor een deeltje dat aan een
stap potentiaal verstrooid. Merk op dat 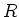 en
en 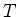 oscillaties vertonen
die veroorzaakt worden door interferenties van de waarschijnlijkheidsgolven
door reflecties aan de discontinuiteiten.
oscillaties vertonen
die veroorzaakt worden door interferenties van de waarschijnlijkheidsgolven
door reflecties aan de discontinuiteiten.



Next: Oneindige Rechthoekige Put Potentiaal
Up: Een-Dimensionale Oplossingen van de
Previous: Stap Potentiaal met
Jo van den Brand
2000-10-21
![]() voor
voor ![]() .
De situatie is geschetst in Fig. 16.
.
De situatie is geschetst in Fig. 16.

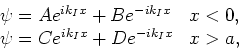
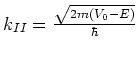 .
Voor
.
Voor 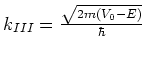 .
.![]() .
.

![]() is de golffunctie grotendeels een staande golf,
maar bevat een kleine bijdrage van een lopende golf, omdat de
gereflecteerde golf een kleinere amplitude heeft dan de inkomende golf.
In het gebied
is de golffunctie grotendeels een staande golf,
maar bevat een kleine bijdrage van een lopende golf, omdat de
gereflecteerde golf een kleinere amplitude heeft dan de inkomende golf.
In het gebied ![]() is de golffunctie een staande golf
waarvan de amplitude exponentieel afneemt. Het meest interessant is
het de coëfficiënt
is de golffunctie een staande golf
waarvan de amplitude exponentieel afneemt. Het meest interessant is
het de coëfficiënt ![]() uit te rekenen, die de verhouding geeft
van de doorgelaten waarschijnlijkheidsflux in het gebied
uit te rekenen, die de verhouding geeft
van de doorgelaten waarschijnlijkheidsflux in het gebied ![]() ten opzichte van de inkomende flux. Een berekening geeft
ten opzichte van de inkomende flux. Een berekening geeft
![\begin{displaymath}
T={v_1{\mathcal{C}}^*{\mathcal{C}} \over v_1 {\mathcal{A}}^*...
...E \over V_0}
\left( 1- {E \over V_0} \right) } \right]^{-1} ,
\end{displaymath}](img450.gif)
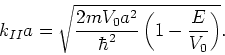
![\begin{displaymath}
T={v_1{\mathcal{C}}^*{\mathcal{C}} \over v_1 {\mathcal{A}}^*...
...E \over V_0}
\left( {E \over V_0} -1 \right) } \right]^{-1} ,
\end{displaymath}](img455.gif)
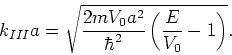

![]() en
en ![]() voor een deeltje dat aan een
stap potentiaal verstrooid. Merk op dat
voor een deeltje dat aan een
stap potentiaal verstrooid. Merk op dat ![]() en
en ![]() oscillaties vertonen
die veroorzaakt worden door interferenties van de waarschijnlijkheidsgolven
door reflecties aan de discontinuiteiten.
oscillaties vertonen
die veroorzaakt worden door interferenties van de waarschijnlijkheidsgolven
door reflecties aan de discontinuiteiten.