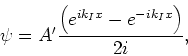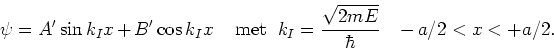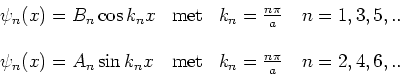Next: LES 05
Up: LES 04
Previous: Tunnel Effect
De potentiaal van een rechthoekige put met oneindig hoge wanden kan
geschreven worden als
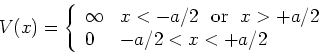 |
(170) |
en wordt geschetst in Fig. 19.
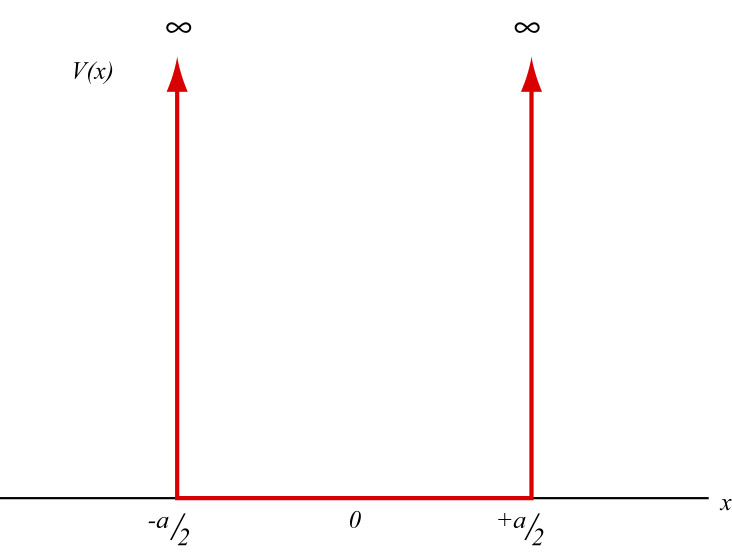 Figure 19:
Schematische weergave van de potentiaal voor een
rechthoekige put met oneindig hoge wanden.
Figure 19:
Schematische weergave van de potentiaal voor een
rechthoekige put met oneindig hoge wanden.
De algemene oplossing van de Schrödingervergelijking
voor een deeltje in het interval
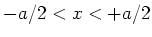 kan geschreven worden als
kan geschreven worden als
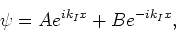 |
(171) |
waarbij het golfgetal gegeven wordt door
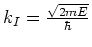 .
We hebben hier te maken met een deeltje dat tussen de beide wanden
heen en weer beweegt en we maken de aanname dat de eigenfunctie in dat
gebied een gelijk mengsel is van golven die in beide richtingen bewegen,
dus
.
We hebben hier te maken met een deeltje dat tussen de beide wanden
heen en weer beweegt en we maken de aanname dat de eigenfunctie in dat
gebied een gelijk mengsel is van golven die in beide richtingen bewegen,
dus 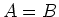 . Dit geeft
. Dit geeft
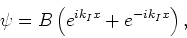 |
(172) |
hetgeen ook geschreven kan worden als
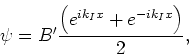 |
(173) |
waar 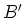 een nieuwe willekeurige constante is, gedefinieerd door
de relatie
een nieuwe willekeurige constante is, gedefinieerd door
de relatie 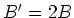 . De eenvoudige combinatie van complexe
exponentiële functies geeft ons
. De eenvoudige combinatie van complexe
exponentiële functies geeft ons
 |
(174) |
We kunnen ook een staande golf construeren door te stellen dat 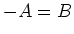 en vinden dan
en vinden dan
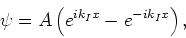 |
(175) |
hetgeen geschreven kan worden als
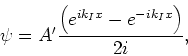 |
(176) |
waar 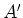 een nieuwe willekeurige constante is, gedefinieerd door
de relatie
een nieuwe willekeurige constante is, gedefinieerd door
de relatie
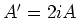 . Dit geeft ons
. Dit geeft ons
 |
(177) |
De Schrödingervergelijking is lineair en we schrijven daarom als
oplossing
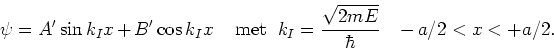 |
(178) |
Merk op dat we vanaf nu de accenten zullen weglaten.
We kunnen eenvoudig nagaan dat we hier met een staande golf te maken
hebben door te kijken naar de volledige golffunctie
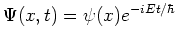 . Verder dient
. Verder dient 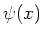 gelijk
aan nul te zijn in het gebied buiten de put, omdat de waarschijnlijkheidsdichtheid
daar gelijk aan nul dient te zijn. Met name aan de grenzen van de put
dient te gelden
gelijk
aan nul te zijn in het gebied buiten de put, omdat de waarschijnlijkheidsdichtheid
daar gelijk aan nul dient te zijn. Met name aan de grenzen van de put
dient te gelden
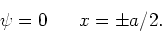 |
(179) |
We vinden twee klassen van oplossingen die aan deze randvoorwaarden voldoen
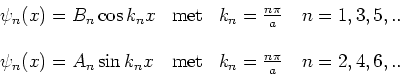 |
(180) |
Het quantumgetal 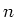 wordt gebruikt om de eigenwaarden te labelen.
Als we verder de relatie
wordt gebruikt om de eigenwaarden te labelen.
Als we verder de relatie
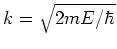 en de uitdrukking
en de uitdrukking 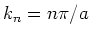 vinden we
vinden we
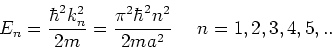 |
(181) |
We zien dat de energieën nu gequantiseerd zijn. Verder vinden we weer
de nulpuntsenergie 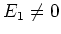 .
.
aap noot



Next: LES 05
Up: LES 04
Previous: Tunnel Effect
Jo van den Brand
2000-10-21
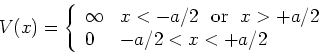
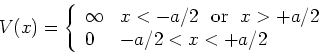

![]() kan geschreven worden als
kan geschreven worden als
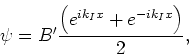

![]() en vinden dan
en vinden dan