


Next: Laguerre polynomen
Up: DIFFERENTIAALVERGELIJKINGEN
Previous: Geassocieerde Legendre differentiaalvergelijking
We willen hier laten zien dat het radiële deel van de oplossing
van de Schrödingervergelijking voor een centrale vierkante
sferische potentiaalput voldoet aan de sferische differentiaalvergelijking
van Bessel. Deze uitdrukking is te vinden op bijvoorbeeld
http://mathworld.wolfram.com/SphericalBesselDifferentialEquation.html
(zie vergelijking (5) aldaar) en luidt
![\begin{displaymath}
r^2{{\rm d}^2R \over {\rm d} r^2} +2r {{\rm d}R \over {\rm d} r}
+ \left[ k^2r^2 - n(n+1) \right] R = 0.
\end{displaymath}](img15.png) |
(6) |
We beginnen de discussie met vergelijking (454) op bladzijde 96
van het dictaat,
![\begin{displaymath}
{{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} \chi \over {...
...\over \hbar^2} \left[ V(r) - E \right] \chi =
l(l+1) \chi .
\end{displaymath}](img16.png) |
(7) |
We gaan een deeltje nu opsluiten in een drie-dimensionale put met
oneindig hoge potentiaal. Voor de potentiaal geldt
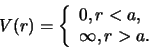 |
(8) |
De golffunctie is dan nul buiten de put, terwijl de golffunctie
binnen de put gegeven wordt door de radiële vergelijking
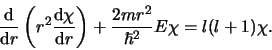 |
(9) |
We kunnen deze vergelijking als volgt herschrijven,
Bovenstaande uitdrukking heeft inderdaad de vorm van de sferische
Bessel differentiaalvergelijking gegeven in uitdrukking (7).



Next: Laguerre polynomen
Up: DIFFERENTIAALVERGELIJKINGEN
Previous: Geassocieerde Legendre differentiaalvergelijking
Jo van den Brand
2004-11-30
![\begin{displaymath}
{{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} \chi \over {...
...\over \hbar^2} \left[ V(r) - E \right] \chi =
l(l+1) \chi .
\end{displaymath}](img16.png)
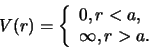
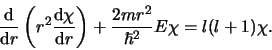
![$\displaystyle {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} \chi \over {\rm d} r} \right)
+ \left[ {2mr^2 \over \hbar^2}E - l(l+1) \right] \chi$](img19.png)
![$\displaystyle {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} \chi \over {\rm d} r} \right)
+ \left[ k^2r^2 - l(l+1) \right] \chi$](img21.png)
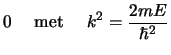
![$\displaystyle r^2{{\rm d}^2 \chi \over {\rm d} r^2} +
2r {{\rm d} \chi \over {\rm d} r}
+ \left[ k^2r^2 - l(l+1) \right] \chi$](img23.png)