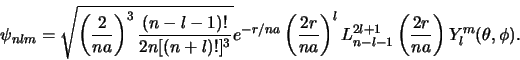Next: About this document ...
Up: DIFFERENTIAALVERGELIJKINGEN
Previous: Sferische Bessel differentiaalvergelijking
Oplossingen van de Schrödingervergelijking voor de Coulomb potentiaal,
dus oplossingen van het waterstofatoom, kunnen geschreven worden als
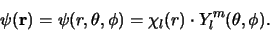 |
(10) |
We zijn hier geïnteresseerd in de radiële golffunctie 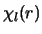 en hebben deze op bladzijde 101, vijfde regel van boven, in het dictaat
geschreven als
en hebben deze op bladzijde 101, vijfde regel van boven, in het dictaat
geschreven als
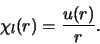 |
(11) |
Vervolgens hebben we in vergelijking (496) een nieuwe functie geïntroduceerd,
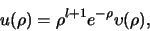 |
(12) |
waarbij overigens
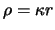 , met
, met
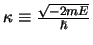 .
De functie
.
De functie
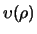 voldoet aan de differentiaalvergelijking
van Laguerre. Deze uitdrukking is te vinden op bijvoorbeeld
http://mathworld.wolfram.com/LaguerreDifferentialEquation.html
(zie vergelijking (2) aldaar) en luidt
voldoet aan de differentiaalvergelijking
van Laguerre. Deze uitdrukking is te vinden op bijvoorbeeld
http://mathworld.wolfram.com/LaguerreDifferentialEquation.html
(zie vergelijking (2) aldaar) en luidt
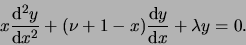 |
(13) |
Deze uitdrukking is van dezelfde vorm als gegeven in vergelijking (499)
op bladzijde 102 van het dictaat:
![\begin{displaymath}
\rho {{\rm d}^2 \upsilon \over {\rm d} \rho^2}
+ 2(l + 1 -...
...{\rm d} \rho}
+ \left[ \rho_0 -2 (l+1) \right] \upsilon = 0.
\end{displaymath}](img33.png) |
(14) |
De uitdrukkingen voor Laguerre polynomen zijn te vinden op bijvoorbeeld
http://mathworld.wolfram.com/LaguerrePolynomial.html
Vergelijking (6) aldaar definieert de Laguerre polynoom als
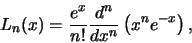 |
(15) |
terwijl de geassocieerde Laguerre polynoom door vergelijking (14)
aldaar gedefinieerd wordt als
![\begin{displaymath}
L_n^k(x) = (-1)^k {d^k \over dx^k} \left[ L_{n+k} (x) \right] .
\end{displaymath}](img35.png) |
(16) |
Afgezien van de normering (de factor 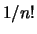 ) komen deze uitdrukkingen
overeen met die gegeven in het dictaat in vergelijking (533) en (532).
Merk op dat in het dictaat dezelfde normering gevolgd wordt als
in de boeken `Quantum Mechanics', Albert Messiah (1961);
`Introduction to Quantum Mechanics', David J. Griffiths (1994).
Op bladzijde 107, zevende regel van beneden, wordt de lezer hierop
geattendeerd (`...afgezien van de normering'). Overigens is
de normering correct uitgevoerd in de golffuncties gegeven in
vergelijking (534) van het dictaat,
) komen deze uitdrukkingen
overeen met die gegeven in het dictaat in vergelijking (533) en (532).
Merk op dat in het dictaat dezelfde normering gevolgd wordt als
in de boeken `Quantum Mechanics', Albert Messiah (1961);
`Introduction to Quantum Mechanics', David J. Griffiths (1994).
Op bladzijde 107, zevende regel van beneden, wordt de lezer hierop
geattendeerd (`...afgezien van de normering'). Overigens is
de normering correct uitgevoerd in de golffuncties gegeven in
vergelijking (534) van het dictaat,
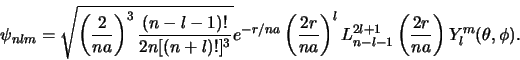 |
(17) |
We herkennen in deze uitdrukking
ook het radiële deel van de oplossing, gegeven door
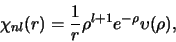 |
(18) |
met
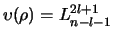 .
.



Next: About this document ...
Up: DIFFERENTIAALVERGELIJKINGEN
Previous: Sferische Bessel differentiaalvergelijking
Jo van den Brand
2004-11-30
![]() ) komen deze uitdrukkingen
overeen met die gegeven in het dictaat in vergelijking (533) en (532).
Merk op dat in het dictaat dezelfde normering gevolgd wordt als
in de boeken `Quantum Mechanics', Albert Messiah (1961);
`Introduction to Quantum Mechanics', David J. Griffiths (1994).
Op bladzijde 107, zevende regel van beneden, wordt de lezer hierop
geattendeerd (`...afgezien van de normering'). Overigens is
de normering correct uitgevoerd in de golffuncties gegeven in
vergelijking (534) van het dictaat,
) komen deze uitdrukkingen
overeen met die gegeven in het dictaat in vergelijking (533) en (532).
Merk op dat in het dictaat dezelfde normering gevolgd wordt als
in de boeken `Quantum Mechanics', Albert Messiah (1961);
`Introduction to Quantum Mechanics', David J. Griffiths (1994).
Op bladzijde 107, zevende regel van beneden, wordt de lezer hierop
geattendeerd (`...afgezien van de normering'). Overigens is
de normering correct uitgevoerd in de golffuncties gegeven in
vergelijking (534) van het dictaat,