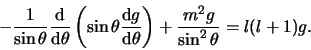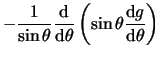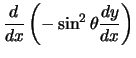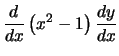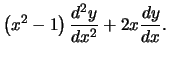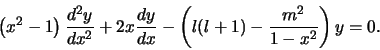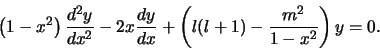Next: Sferische Bessel differentiaalvergelijking
Up: DIFFERENTIAALVERGELIJKINGEN
Previous: DIFFERENTIAALVERGELIJKINGEN
De geassocieerde Legendre differentiaalvergelijking geeft de
oplossing van het 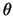 -deel van de hoekafhankelijkheid
van de Schrödingervergelijking voor een centrale potentiaal.
Deze uitdrukking is te vinden op bijvoorbeeld
http://mathworld.wolfram.com/LegendreDifferentialEquation.html
(zie vergelijking (22) aldaar) en luidt
-deel van de hoekafhankelijkheid
van de Schrödingervergelijking voor een centrale potentiaal.
Deze uitdrukking is te vinden op bijvoorbeeld
http://mathworld.wolfram.com/LegendreDifferentialEquation.html
(zie vergelijking (22) aldaar) en luidt
![\begin{displaymath}
(1-x^2){{\rm d}^2y \over {\rm d} x^2} -2x {{\rm d}y \over {\rm d} x}
+ \left[ l(l+1) - {m^2 \over 1- x^2} \right] y = 0.
\end{displaymath}](img2.png) |
(1) |
We willen hier laten zien dat dit overeenkomt met uitdrukking (440)
op bladzijde 94 van het dictaat.
We beginnen de discussie met vergelijking (440) op bladzijde 96
van het dictaat,
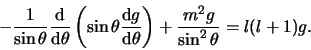 |
(2) |
We definiëren
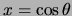 en dus
en dus
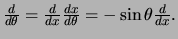 Verder stellen we
Verder stellen we 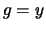 . Hiermee kunnen we schrijven
. Hiermee kunnen we schrijven
We definiëren
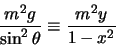 |
(3) |
en vinden nu als differentiaalvergelijking
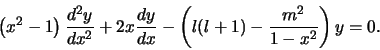 |
(4) |
We kunnen dit schrijven als
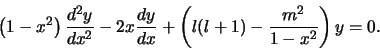 |
(5) |
Bovenstaande uitdrukking is identiek aan de geassocieerde Legendre
differentiaalvergelijking gegeven door uitdrukking (1).



Next: Sferische Bessel differentiaalvergelijking
Up: DIFFERENTIAALVERGELIJKINGEN
Previous: DIFFERENTIAALVERGELIJKINGEN
Jo van den Brand
2004-11-30
![\begin{displaymath}
(1-x^2){{\rm d}^2y \over {\rm d} x^2} -2x {{\rm d}y \over {\rm d} x}
+ \left[ l(l+1) - {m^2 \over 1- x^2} \right] y = 0.
\end{displaymath}](img2.png)