5. Optical transitions in a two-level system

Einstein, in his pivotal paper of 1917, discussed the radiation balance in a generalized two-level system. Here he postulated the concept of stimulated emission, in addition to the intuitively understood concepts of absorption and spontaneous emission.

A. Einstein Nobel Prize laureate 1921

Involved are two levels, with energies E₂ (upper) and E₁ (lower) and populations n₂ and n₁. The radiation field at frequency v (monochromatic), with energy density u_v is considered to be resonant with the energy separation: E₂ - E₁ = hv.

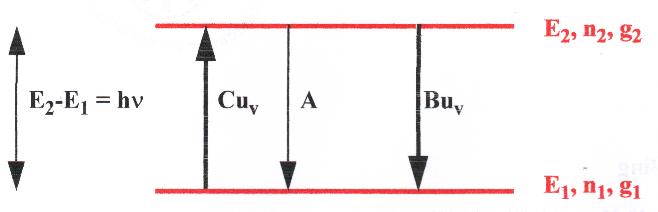
Einstein defined three processes:

Absorption; this process is proportional to the population of the ground state and the density of the radiation field u_v; a proportionality constant is defined as C.

Spontaneous emission; this process is only proportional to the population of the excited state and not to a radiation field density; the proportionality constant is A.

Stimulated emission; maybe counter intuitively, Einstein defined a process of emission induced by the radiation field; it is proportional to the population density n₂ as some inverse absorption process; the proportionality constant is B.

The three proportionality constants A, B and C are the "Einstein coefficients".

---

Then rate equations can be written for the population of the states:

dn₂/dt = Cu_vn₁ - (A + Bu_v)n₂
In the steady state condition (dn₂/dt = 0) this gives:
n₁/n₂ = (A + Bu_v) / Cu_v
Now, as a result from statistical phsyics, for the case of thermodynamic equilibrium at temperature T, the Maxwell-Boltzman distribution defines the probability that a level is thermally excited.
Hence:
n₁/n₂ = exp(-E₁/kT) / exp(-E₂/kT) = exp(hv/kT)
where k is the Boltzmann constant.

When it is now assumed that the (atomic) two-level system is in thermodynamic equilibrium with its environment at temperature T, the two equations for the ratio n₁/n₂ yield an equation for the radiation field expressed in terms of the Einstein coefficients; this procedure can be understood as the radiative processes creating the equilibrium:

u_v = A / (Cexp(hv/kT) - B)
For radiative balance between a body at temperature T and a radiation field u_v Planck's radiation formula should hold. Indeed the formula for u_v has the structure of Planck's equation. The derived equation for u_v agrees with that of Planck if the following simple relations between the Einstein coefficients are adopted:

B = C; so stimulated emission is equally "strong" as absorption

A/B = 8(pi)hv³/c³; giving a relation between spontaneous and stimulated emission

The Einstein B-coefficient, or the strength of an absorption line, should be proportional to the square of the transition amplitude, i.e. the expectation value of the transition dipole moment. The exact formula can be derived from a quantummechanical treatment of the interaction between light and matter. Without proof we give:


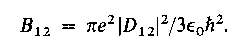
The coefficient for spontaneous emission then automatically follows from the above derivation of the Einstein coefficients:


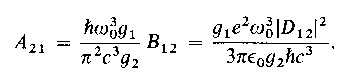
Note that the factors g₁ and g₂ denote the degeneracy of the levels, i.e. a factor of 3 for a p-state, a 1 for an s-state.

---

The above has some interesting physical consequences

Last change: 8 February 2001