Some interesting physical consequences of the Einstein model:

In the absence of a radiation field (u_v = 0) the dynamical rate equations reduce to:
dn₂/dt = -An₂.
With the boundary condition n₂(0) = N, so initially all population in the excited state, this gives an exponential decay function, with A as the decay rate. Note that an excited level in a multi-level atom can decay in various ways following certain branching ratios, that are defined by the quantum mechanical transition rates. In the picture the decay rates for levels in hydrogen are displayed. The numbers are in 10⁶ s^-1.


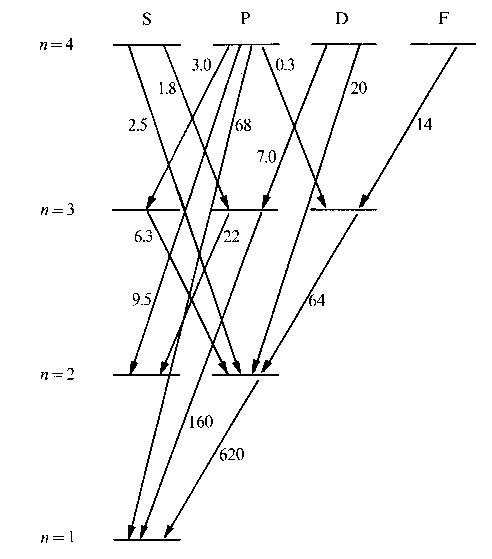
So A is the inverse of the radiative lifetime of the excited state. In case of branching ratios the lifetime relates to the SUM of the decays.

For all densities of the radiation field u_v the inequality holds:

C u_v < A + B u_v

Even without explicitly solving the dynamical rate equations it is intuitively understandable that for a boundary condition n₁(0) = N, so all population initially in the ground state, the situation n₂ > n₁ can never be reached. Stated in other words: a population inversion cannot be achieved via optical pumping.
Or: an optically pumped two-level laser is not possible.


From the perspective of quantum emchanics it is well understandable that the processes of absorption and stimulated emission sale with the same constant. It is the same transition dipole moment that governs both transitions. The eqaulity B=C sets the excited and ground state on an equal footing. The solutions of the time-independent Schrodinger equation are stationary states and there is no straightforward explanation for the process of "spontaneous emission". In principle stationary states do NOT decay. The resolution of this contradiction lies in the theory that goes beyong quantum mechanics: QED. There spontaneous emission is viewed upon as stimulated by the photons created by the vacuum polarization.

Last change: 18 February 2001