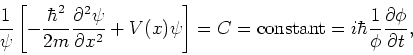Next: Tijdsonafhankelijke Schrödingervergelijking
Up: Een-Dimensionale Oplossingen van de
Previous: Een-Dimensionale Oplossingen van de
In het vervolg van dit hoofdstuk zullen we trachten enkele oplossingen
te vinden van de Schrödingervergelijking. We beperken de discussie
tot één-dimensionale gevallen. Allereerst passen we de techniek
van het scheiden van variabelen toe, teneinde een oplossing te vinden
voor het tijdsafhankelijke deel van de golffunctie. We stellen dat
de volledige toestandsfunctie beschreven wordt door
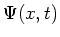 , die voldoet aan
, die voldoet aan
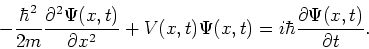 |
(112) |
We beschouwen in het vervolg een statische potentiaal 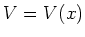 en schrijven de toestandsfunctie als een product van twee factoren
en schrijven de toestandsfunctie als een product van twee factoren
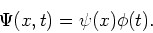 |
(113) |
Invullen in de Schrödingervergelijking levert
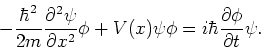 |
(114) |
Delen door het product 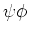 levert de vergelijking
levert de vergelijking
![\begin{displaymath}
{1 \over \psi} \left[ -{\hbar^2 \over 2m}{\partial^2 \psi \o...
...ght] = i\hbar {1 \over \phi} {\partial \phi \over \partial t}.
\end{displaymath}](img343.gif) |
(115) |
De linkerzijde van bovenstaande uitdrukking hangt enkel af van 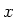 , terwijl
de rechterzijde uitsluitend afhangt van
, terwijl
de rechterzijde uitsluitend afhangt van 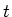 . De gelijkheid dient te gelden
voor elke
. De gelijkheid dient te gelden
voor elke 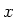 en
en 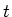 en hieruit kunnen we concluderen dat
en hieruit kunnen we concluderen dat
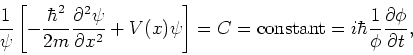 |
(116) |
waarbij 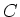 de zogenaamde scheidingsconstante is.
de zogenaamde scheidingsconstante is.
De oplossing van het tijdsafhankelijke deel kan eenvoudig verkregen
worden. We vinden de eerste-orde differentiaalvergelijking
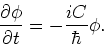 |
(117) |
We proberen als oplossing de functie
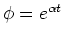 met als afgeleide
met als afgeleide
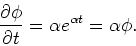 |
(118) |
Invullen levert
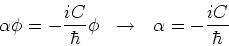 |
(119) |
en dus geldt
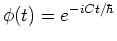 . Verder geldt
. Verder geldt 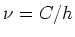 en vinden we voor de scheidingsconstante
en vinden we voor de scheidingsconstante 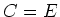 .
.
Het tijdsafhankelijke deel van de oplossing is dus
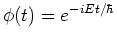 . . |
| |



Next: Tijdsonafhankelijke Schrödingervergelijking
Up: Een-Dimensionale Oplossingen van de
Previous: Een-Dimensionale Oplossingen van de
Jo van den Brand
2000-10-21
![]() , die voldoet aan
, die voldoet aan
![\begin{displaymath}
{1 \over \psi} \left[ -{\hbar^2 \over 2m}{\partial^2 \psi \o...
...ght] = i\hbar {1 \over \phi} {\partial \phi \over \partial t}.
\end{displaymath}](img343.gif)