


Next: About this document ...
Up: hovo
Previous: hovo
ORTHOGONALITEIT
In het volgende willen we enkele opmerkingen maken met betrekking tot de orthogonaliteit van de golffuncties van het waterstofatoom. Allereerst definiëren we de zogenaamde Bohrstraal als
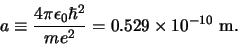 |
(1) |
Hiermee kunnen we de genormeerde golffuncties voor het waterstofatoom schrijven als
 |
(2) |
met
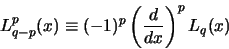 |
(3) |
de geassocieerde Laguerre polynoom en
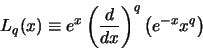 |
(4) |
de 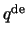 Laguerre polynoom.
Laguerre polynoom.
De oplossingen zijn onderling orthogonaal,
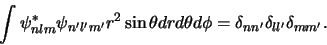 |
(5) |
Merk op dat golffuncties orthogonaal zijn als het hoofdquantumgetal 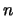 verschillend is. Voor twee golffuncties met gelijk hoofdquantumgetal zorgen de sferisch harmonische functie
verschillend is. Voor twee golffuncties met gelijk hoofdquantumgetal zorgen de sferisch harmonische functie
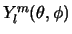 voor de orthogonaliteit. Merk verder op dat in de integraal1 voor orthogonaliteit het volume-element
voor de orthogonaliteit. Merk verder op dat in de integraal1 voor orthogonaliteit het volume-element 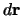 geschreven wordt als
geschreven wordt als
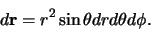 |
(6) |
De orthogonaliteit van de sferisch harmonische functies hebben we expliciet afgeleid. De functies
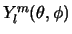 kunnen geschreven worden als
kunnen geschreven worden als
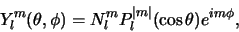 |
(7) |
waarbij de laagste-orde sferisch harmonische functies worden gegeven door
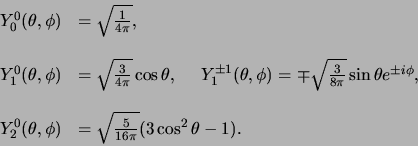 |
(8) |
We weten dat de functies 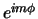 orthogonaal zijn (zie bijvoorbeeld hoofdstuk 2 over Fourieranalyse). We hebben ook laten zien dat de Legendre polynomen
orthogonaal zijn (zie bijvoorbeeld hoofdstuk 2 over Fourieranalyse). We hebben ook laten zien dat de Legendre polynomen
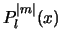 orthogonaal zijn: dat is gedemonstreerd in paragraaf 7.1.2, waarbij het niet uit maakt dat we voor
orthogonaal zijn: dat is gedemonstreerd in paragraaf 7.1.2, waarbij het niet uit maakt dat we voor
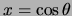 kiezen.
kiezen.
Figuur 1:
Radiële golffuncties voor het elektron in het waterstofatoom voor diverse quantumgetallen 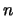 en
en 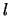 . Het bereik loopt van
. Het bereik loopt van 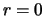 tot
tot 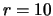 Å.
Å.
|
|
Het rest ons dus om aan te tonen dat ook de radiële golffuncties (voor verschillende 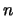 ) orthogonaal zijn.
) orthogonaal zijn.
De laagste-orde radiële golffuncties van een één-elektron atoom kunnen expliciet geschreven worden als
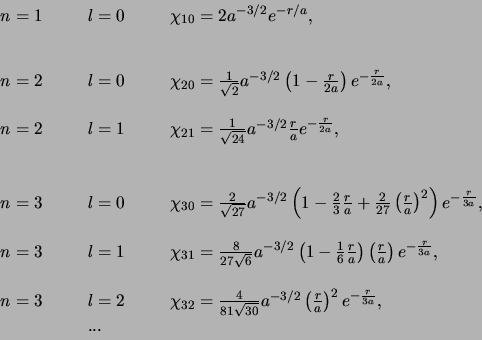 |
(9) |
Enkele radiële golffuncties voor het elektron in het waterstofatoom zijn weergegeven in Fig. 1. Merk op dat enkele van deze functies zowel een positieve als negatieve bijdrage hebben.
Fig. 2 toont de corresponderende radiële waarschijnlijkheidsdichtheden voor het waterstofatoom.
Figuur 2:
De radiële waarschijnlijkheidsdichtheid voor het elektron in het waterstofatoom voor diverse quantumgetallen 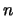 en
en 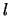 .
.
|
|
De totale waarschijnlijkheid om een elektron in een baan aan te treffen wordt gegeven door
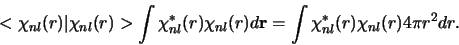 |
(10) |
De waarschijnlijkheidsdichtheden getoond in Fig. 2 komen overeen met de integrand
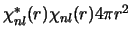 van vergelijking (10).
van vergelijking (10).
Tenslotte laten we de orthogonaliteit expliciet zien voor de radiële golffuncties 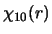 en
en 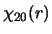 . De functies zijn geplot in Fig. 1. Orthogonaliteit betekent
. De functies zijn geplot in Fig. 1. Orthogonaliteit betekent
Figuur 3:
De integrand van vergelijking (11) wordt getoond als functie van 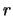 . De totale sum is gelijk aan nul.
. De totale sum is gelijk aan nul.
|
|
Figuur 3 toont de integrand van vergelijking (11) als functie van 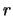 . De totale sum is gelijk aan nul, waarbij bewezen is dat de radiële functies
. De totale sum is gelijk aan nul, waarbij bewezen is dat de radiële functies 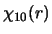 en
en 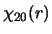 orthogonaal zijn.
orthogonaal zijn.



Next: About this document ...
Up: hovo
Previous: hovo
Jo van den Brand
2004-11-27

![]() kunnen geschreven worden als
kunnen geschreven worden als 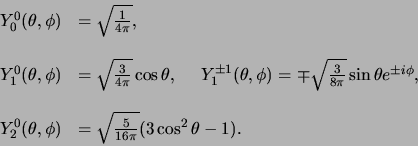
![\includegraphics[width=15cm]{Figures/radwave.eps}](img21.png)
![]() ) orthogonaal zijn.
) orthogonaal zijn.
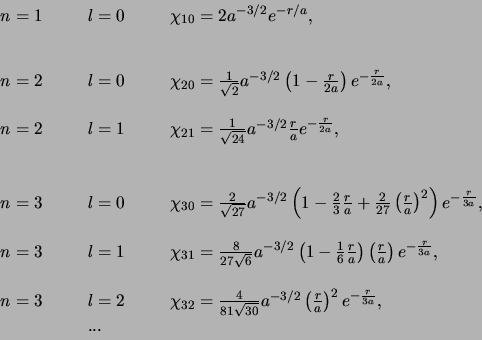
![\includegraphics[width=14cm]{Figures/Fig26.eps}](img23.png)
![]() en
en ![]() . De functies zijn geplot in Fig. 1. Orthogonaliteit betekent
. De functies zijn geplot in Fig. 1. Orthogonaliteit betekent ![\includegraphics[width=15cm]{Figures/ortho.eps}](img35.png)