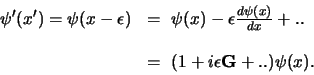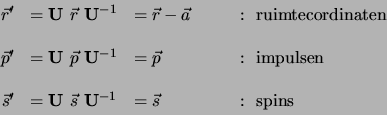Next: Behoud van lading
Up: SYMMETRIEËN
Previous: Inleiding
Contents
Voor een continue transformatie is het efficiënt een additionele
operator (een zogenaamde generator) G in te voeren,
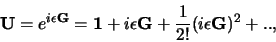 |
(678) |
waarbij 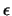 een reëele grootheid is. Uit de unitariteit van
een reëele grootheid is. Uit de unitariteit van
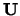 volgt dan dat
volgt dan dat
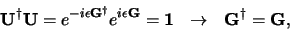 |
(679) |
en we vinden dat de hermitische operator 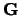 de gezochte
behouden grootheid vertegenwoordigt.
Indien U met een symmetrietransformatie overeenkomt,
de gezochte
behouden grootheid vertegenwoordigt.
Indien U met een symmetrietransformatie overeenkomt,
![$[ {\bf H, U} ] = 0$](img1977.png) , dan vinden we in de limiet van een infinitesimale
transformatie,
, dan vinden we in de limiet van een infinitesimale
transformatie,
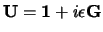 , direct de relatie
, direct de relatie
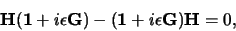 |
(680) |
en dus
![\begin{displaymath}[ {\bf H, G} ]= 0.
\end{displaymath}](img1980.png) |
(681) |
Figuur 50:
Illustratie van een symmetrietransformatie aan de hand van
de translatie van de golffunctie van een deeltje. Het pakket verschuift
over een afstand 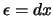 .
.
|
|
We zullen deze procedure toelichten aan de hand van een eenvoudig
voorbeeld. We beschouwen in figuur 50
de translatie van de golffunctie van een deeltje in één dimensie.
We eisen, dat voor een waarnemer in het getransleerde coördinatensysteem
dezelfde wetten gelden42, en dus
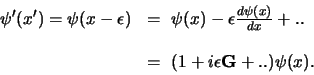 |
(682) |
Hiermee vinden we
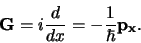 |
(683) |
De operator 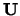 commuteert met de Hamiltoniaan
commuteert met de Hamiltoniaan 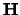 , en
daarmee dan ook
, en
daarmee dan ook 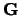 , die evenredig is met de impulsoperator
, die evenredig is met de impulsoperator
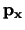 . De hiermee corresponderende observabele
. De hiermee corresponderende observabele 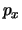 is de
gezochte behouden grootheid.
is de
gezochte behouden grootheid.
In het algemeen vertegenwoordigt de translatieoperator
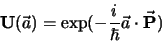 |
(684) |
de volgende transformaties (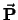 is de totale impuls van het
systeem),
is de totale impuls van het
systeem),
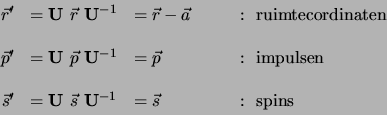 |
(685) |




Next: Behoud van lading
Up: SYMMETRIEËN
Previous: Inleiding
Contents
Jo van den Brand
2004-09-25
![\includegraphics[width=8cm]{Figures/psim1.eps}](img1981.png)