Spin-orbit coupling

The spin-orbit coupling may be treated in a similar fashion as for one-electron atoms. The total angular momentum quantum number J = L + S will of course be used and proper eigenfunctions are those of L², S², J² and J_z. We call these, which are the correct zero order functions,

The first order correction to the energy E_s-o is then given by

J may take all integer values between L+S and |L-S| which means that the spin-orbit coupling splits a term into either 2L+1 or 2S+1 fine structure levels. Since the energy is independent of M, every level will have (2J+1)-fold degeneracy.

As for one-electron atoms, the spin-orbit coupling may be expressed in terms of the different angular momenta using

where A(L,S) is called the interval factor. The distance between adjacent fine structure levels J and J-1 is obtained as

This is the Landé interval rule.

Use the result from first order perturbation theory to determine the energy of the fine structure levels in ³P-state from a p²-configuration.

We have the following values of the quantum numbers: L=1, S=1, J=0,1,2

Inserting L and S gives the formula

with the following energies:

J
2	A
1	-A
0	-2A

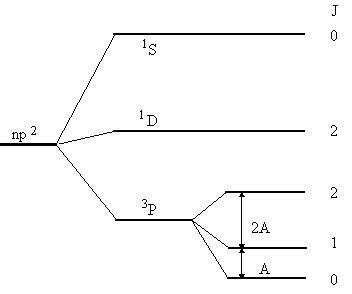
The spin-orbit splitting has been exaggerated in order to make a legible figure. Of course, spin-orbit splittings may be of this size for heavy atoms, but the perturbation treatment may then be less appropriate.

These energy levels are: E(³P₀) = 0 eV; E(³P₁) = 0,00203 eV; E(³P₂) = 0,00539 eV;E(¹D₂) = 1,26386 eV; E(¹S₀) = 2,68406eV;