The SCF method.

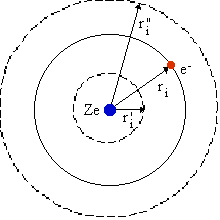
An apprehension about the potential V_i(r_i) in the Hamiltonian can be obtained using ordinary classical electrostatics. We consider a central symmetric field and draw a simple figure as shown below and derive for this geometry the average potential experienced by the electron at a distance r_i from the nucleus.

The interaction with electronic charges at smaller and larger radius than r_i as well as the nucleus are indicated in the figure. The contribution to the potential from each of these is (expressed in a.u.)

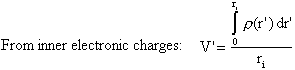
The charge density is obtained from the wavefunctions in the usual manner as

Inserting this in the expression for the potential gives

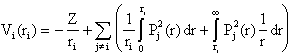
Hence, the potential will depend upon all other electrons, i.e. we obtain a system of coupled integral-differential equations. The integrals can be calculated if the radial wavefunctions are known. Of course, they are not since it is these function we want to determine. However, they can be derived in an iterative process, where one starts from guessed functions and carries out calculations which improve the wavefunctions until convergence has been achieved. This is called the SCF-method (Self-Consistent-Field). The procedure may look like this:

When convergence has been reached, the solutions are said to be self consistent. In Hartree's method, the total wavefunction is a simple product function which does not comply with the Pauli exclusion principle, as already mentioned. The use of the proper antisymmetrised wavefunctions (Slater determinants) lead to the so-called Hartree-Fock method.

Finally, it may be noted again that all closed shells give rise to a symmetric charge distribution. The only non-central contributions to the potential arise from the electrons of unfilled shells with an angular momentum quantum number l > 0. For atoms being in the ground state, there is usually only one such shell, so the asymmetry in the charge distribution may be rather small. This apparently explains much of the success of the central field approximation.