The Zeeman effect
The explanation of the spectrum of the hydrogen atom was a leap forward, made possible by
quantum mechanics. However, the spectra of other elements were not yet explained.
Moreover some subtle effects were observed already at the beginning of the 20th century,
for which no explanation existed. Zeeman investigated spectral lines in a magnetic field
and observed some interesting phenomena:
Normal Zeeman effect: the splitting of a spectra line into 3 components for which Lorentz
provided an explanation based on classical electrodynamics.
Read: Lorentz's explanation
Anomalous Zeeman effect: splitting of a spectra line into 2, 4 or more components,
for which no classical explanation existed.
Observation of "Zeeman spectra"
Splitting of spectral lines (fine structure) even in the absence of a magnetic field.
P. Zeeman and H.A. Lorentz
Nobel Prize laureates 1902
Magnetic effects and quantum mechanics
In quantum mechanics shifts of energy levels are not explained by referring to oscillatory motion
of electrons (Lorentz model), but rather in terms of change of energy (or potential).
The magnetic interaction energy of a magnetic dipole in a magnetic field
can be added to the energy of the system.
The magnetic dipole moment may be described in a semiclassical way by
relating it to the (quantized) orbital angular momentum vector.
Study: Electronic orbital magnetic moment
Some g-factor of g=1 is defined for the orbital angular momentum,
having no special meaning.
It can be understood from a classical analysis of charges moving in orbit.
The
Bohr magneton
is defined as the atomic unit of energy per magnetic field strength.
Study again the
vector model for orbital angular momentum
Vector L undergoes a Larmor-precession in the presence of a magnetic field (around
the magnetic field vector B).
Theory of the normal Zeeman effect
Now the Zeeman effect can be easily calculated. The expectation value
of the magnetic dipole moment is proportional to that of
Lz giving l different values of ml;
these m-components are split in energy by the Bohr magneton times B.
Study: quantummechanical analysis of the Zeeman-effect
Note that it is of crucial importance that the Zeeman term in the Hamiltonian,
used as an operator, does not change the eigenfunction. Only under this condition
the expectation values of Lz can be straightforwardly calculated.
Necessity for introducing another quantum number
The Stern-Gerlach experiment
(see details) examines the dynamics of a magnetic dipole in a
nonuniform magnetic field. A magnetic dipole undergoes a force if the
field is not uniform.
The result of the Stern-Gerlach experiment is that an intrinsic two-valued
parameter is found in some atoms (such as Ag or H) giving rise to two-fold
images in the experiment.
Pauli could explain the structure of multiplets and the anomalous Zeeman effect
on the basis of such an additional quantum number (see below)
Goudsmit and Uhlenbeck proposed
(see original paper)
that this two-valued parameter was an intrinsic
property of the electron that behaves like an angular momentum.
They referred to this property as
electron spin imagining (in a classical picture that must be wrong)
a spinning motion of the electron around its internal axis.
Associated with the electron spin is again a so-called g-factor,
that has a value close to 2. Relativistic quantum mechanics
(Diracs theory) yields exactly 2, while the contributions of QED
give a small deviation. This
g-factor relates the spin to the resulting magnetic moment
of the electron.
S. Goudsmit
G.E. Uhlenbeck
Addition of angular momenta L and S
The two angular momenta L and S can be both viewed in a
vector model.
In the presence of a magnetic field both vectors precess independently
around the B-vector, when interaction between L and S is ignored.
In that case the momenta can be added to form a vector J = L + S
as displayed. Read
vector coupling
Spin-orbit interaction
A semiclassical treatment of the spin-orbit interaction calculates the magnetic interaction
between the spin S of the electron that interacts with the magnetic field produced
by the orbital motion L of the electron itself.
1st step:
Calculation of the effective B-field of an orbit with L
using the
Biot-Savart law.
2nd step: Calculation of the potential energy of a magnetic
(electron spin) moment in the
internal B-field produced by the orbit.
Derivation
Note that this derivation has a flaw because of the non-relativistic
treatment of the electronic motion. In a correct analysis (by Thomas)
an additional factor 1/2 is found for the spin-orbit interaction energy,
resulting in the correct expression:
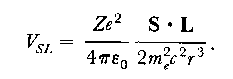
Based on this interaction term the energy shifts induced by the spin-orbit interaction
can be calculated.
Calculation
And the
fine structure in the 2p state of atomic hydrogen can be calculated.
Spin-orbit interaction and the relativistic correction
The kinematic relativistic effects, related to the speed of the electron, have a small influence
on the spectroscopy of the hydrogen atom. The
Relativistic correction can be expanded in tersm of the kinetic energy operator
in a perturbation series. Using the first order this gives rise to
relativistic energy shifts of the hydrogenic levels.
It turns out that the relativistic correction and the spin-orbit interaction have
a similar size in the n=2 state of the hydrogen atom;
read.
Zeeman effect for coupled angular momenta
The problem of the spin-orbit interaction is that
L and S are no longer "good quantum numbers" and that in fact the total angular
monetum J has to be included in the analysis of the Zeeman effect.
In the vector model this can be understood as the vector J precessing around
the magnetic field vector B, while L and S become decoupled.
Vector model for J
In a strong magnetic field however the spin-orbit interaction is relatively small
and can be ignored. In that case the individual contributions from the magnetic moments
originating from spin and orbit vcan be included separately. Note that the total
magnetic moment scales with L + 2S, if the spin g-factor is set to 2.
Hence the energy levels scale with (ml+2ms);
this limiting case in the
Paschen-Back limit.
At weaker fields a problem arises because the g-factors of the spin and
orbital angualr momenta are different. As a result the magnetic moment
(the sum) is not directed along the J-vector and therefore the total
g-factor becomes a complicated fucntion of both contributions.
A proper analysis of this problem gives the
Lande factor, which is a fcuntion of the J, L and S quantum numbers.
Using this anomalous g-factor the fine structure splittings of many atoms
can be calculated; here is an example for the
Na atom.
Hyperfine effects of magnetic coupling
The fact that nuclei have spins, just like the electron, gives rise to further
magnetic effects in the atoms and their spectra. The nuclear magneton as a unit
of this interaction scales however with the inverse of the mass of the particle
and is therefore much smaller. Hence the interaction is smaller, therefore the name
"hyperfine".
The g-factors of the nuclei, including of the bare proton and neutron, is an entire
story. They result from the internal structure of the particle, built of quarks,
and are experimentally determined.
Analysis of hyperfine structure
Last change: 18 February 2001
Normal Zeeman effect: the splitting of a spectra line into 3 components for which Lorentz
provided an explanation based on classical electrodynamics.
Read: Lorentz's explanation
Anomalous Zeeman effect: splitting of a spectra line into 2, 4 or more components,
for which no classical explanation existed.Observation of "Zeeman spectra"
Splitting of spectral lines (fine structure) even in the absence of a magnetic field.
P. Zeeman and H.A. Lorentz
Nobel Prize laureates 1902
Some g-factor of g=1 is defined for the orbital angular momentum,
having no special meaning.
It can be understood from a classical analysis of charges moving in orbit.
The
Bohr magneton
is defined as the atomic unit of energy per magnetic field strength.
Study again the
vector model for orbital angular momentum
Vector L undergoes a Larmor-precession in the presence of a magnetic field (around
the magnetic field vector B).
Pauli could explain the structure of multiplets and the anomalous Zeeman effect
on the basis of such an additional quantum number (see below)
Goudsmit and Uhlenbeck proposed
(see original paper)
that this two-valued parameter was an intrinsic
property of the electron that behaves like an angular momentum.
They referred to this property as
electron spin imagining (in a classical picture that must be wrong)
a spinning motion of the electron around its internal axis.Associated with the electron spin is again a so-called g-factor, that has a value close to 2. Relativistic quantum mechanics (Diracs theory) yields exactly 2, while the contributions of QED give a small deviation. This g-factor relates the spin to the resulting magnetic moment of the electron.
S. Goudsmit
G.E. Uhlenbeck
1st step:
Calculation of the effective B-field of an orbit with L
using the
Biot-Savart law.
2nd step: Calculation of the potential energy of a magnetic
(electron spin) moment in the
internal B-field produced by the orbit.
DerivationNote that this derivation has a flaw because of the non-relativistic treatment of the electronic motion. In a correct analysis (by Thomas) an additional factor 1/2 is found for the spin-orbit interaction energy, resulting in the correct expression:
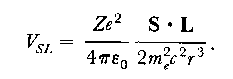
Based on this interaction term the energy shifts induced by the spin-orbit interaction can be calculated. Calculation
And the fine structure in the 2p state of atomic hydrogen can be calculated.
In a strong magnetic field however the spin-orbit interaction is relatively small
and can be ignored. In that case the individual contributions from the magnetic moments
originating from spin and orbit vcan be included separately. Note that the total
magnetic moment scales with L + 2S, if the spin g-factor is set to 2.
Hence the energy levels scale with (ml+2ms);
this limiting case in the
Paschen-Back limit.
At weaker fields a problem arises because the g-factors of the spin and
orbital angualr momenta are different. As a result the magnetic moment
(the sum) is not directed along the J-vector and therefore the total
g-factor becomes a complicated fucntion of both contributions.
A proper analysis of this problem gives the
Lande factor, which is a fcuntion of the J, L and S quantum numbers.
Using this anomalous g-factor the fine structure splittings of many atoms
can be calculated; here is an example for the
Na atom.