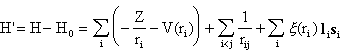
LS-coupling

When there are unfilled shells in an atom, there may be possibilities to form wavefunctions that correspond to different electronic states for a given configuration. To get a good understanding of the electronic structure, we must be able to define these states and determine how they are energetically ordered.

The answers are found by investigating the non-central contributions to the field and the spin-orbit coupling. The Hamiltonian to be considered is defined by the difference between the full operator and H₀, i.e.

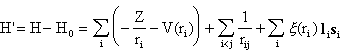
We assume that the central contributions to the integral from the first term and substantial parts of the second have been obtained by the SCF procedure. Alternatively, we may simply neglect them, since in this connection we are only interested in describing the splitting of a configuration into different electronic states. The interesting part of H' is now rather small and may be treated as a perturbation operator.

To proceed systematically, we treat the influence of electron-electron interaction and spin-orbit coupling separately. We start by the former, i.e. consider such atoms where the spin-orbit coupling is considered to be small compared to the electron-electron interaction H_es

Exercise: The splitting of a configuration into different levels presumes a certain degree of degeneracy, i.e. the configuration must contain two or more states that all have the same energy. A configuration may be strongly degenerate. Derive the degree of degeneracy for an (np n'p) -configuration when nn'.

For the perturbation calculation we need wavefunctions which diagonalises the operator H_es within the configuration. These functions can be expanded as linear combinations of eigenfunctions within the configuration as

and are the correct zero order wavefunctions. They provide in a perturbation calculation the first order correction to the energy within the configuration, i.e.

To find these functions we look for the operators that commute with the Hamiltonian H_es. The simultaneous eigenfunctions to these and the Hamiltonian form a proper basis for the expansion of the wavefunctions. The way to handle this problem and to determine the energy of the various states will be shown in a higher level course. Here we shall focus our attention primarily on the question which states may arise from a configuration and see how we may determine the energy ordering between different states using qualitative arguments.

H_es does not commute with l_i for the individual electrons, but with the total orbital angular momentum operator L where we have

It may also be shown that H_es commutes with L_z and L². H_es commutes also with the total spin operator S where

as well as with the individual spins, which readily realised since H_es does not depend upon the spin. In addition, all these angular momenta commute with H₀.

A proper choice of basis functions is therefore the simultaneous eigenfunctions to H₀, i.e. L², S², L_z and S_z. The correct zero order eigenfunctions are written

where designates the configuration and eigenvalues associated with this. The angular momenta L², S², L_z and S_z are constants of motion in this approximation and L and S are good quantum numbers.

The following relationships apply for M_L and M_S

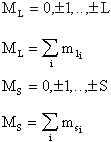
It can be shown that L = S = 0 for closed subshells.

The first order contribution to the energy is thus

It may be shown that the splitting of the configuration does not depend on M_L and M_S but only of L and S. The energy levels which are characterised by certain values of L and S are called terms and the coupling of angular momenta of individual electrons to a resulting orbital angular momentum and spin is referred to as LS-coupling or Russell-Saunders coupling.

A useful scheme for identification of the terms that may arise for a given configuration is shown in the example below. It contains the quantum numbers M_L, M_S, m_li and m_si where the index i refers to individual electrons. The quantum state for separate electrons is defined by the symbol

where m_s can only take either of the values +1/2 or -1/2 and therefore is indicated with a + or - sign.

Determine the terms that may arise for a neon atom in an excited state with the following configuration: 1s² 2s² 2p⁵ 3p.

We first notice that we have two filled subshells (1s and 2s), which both give ¹S₀. We may therefore focus on the two p-shells. For the p⁵-configuration it is not necessary to consider five electrons but just the p-vacancy. Thus, the terms are those arising for two non-equivalent electrons forming an np n'p configuration. We label the quantum states

and construct the following scheme were all wavefunctions are included.

np n'p		MS
		1	0		-1
ML	2	(1+ 1+)	(1+ 1-)	(1- 1+)	(1- 1-)
	1	(1+ 0+) (0+ 1+)	(1+ 0-) (1- 0+)	(0+ 1- ) (0- 1+)	(1- 0-) (0- 1-)
	0	(1+ -1+) (0+ 0+) (-1+ 1+)	(1+ -1-) (0+ 0-) (-1+ 1-)	(1- -1+) (0- 0+) (-1- 1+)	(1- -1-) (0- 0-) (-1- 1-)
	-1	(-1+ 0+) (0+ -1+)	(-1+ 0-) (-1- 0+)	(0+ -1-) (0- -1+)	(-1- 0-) (0- -1-)
	-2	(-1+ -1+)	(-1+ -1-)	(-1- -1+)	(-1- -1-)

The possible states obtained in this scheme are ³D, ³P, ³S, ¹D, ¹P, ¹S. Most of these states are strongly degenerate since the energy is independent of M_L and M_S. The degree of degeneracy is obtained by the product (2L+1)(2S+1) for each term. Hence, the total number of states are 15+9+3+5+3+1=36. They must apparently represented in some form in the table and if we count them all the result is surely 36.

Determine the terms that may arise for a neon atom in an excited state with the following configuration: 1s² 2s² 2p⁵ 3d.

In the above example, the Pauli exclusion principle is automatically accounted for since the two p electrons belong to different shells (the electrons are non-equivalent), i.e. they have different principle quantum numbers. However, in cases where this is not true and the electrons belong to the same subshell (the electrons are equivalent), the situation becomes somewhat more complicated. Some of the states that arise when all possible combinations of the quantum numbers are formed must then perhaps be omitted to comply with the Pauli principle.

Determine the terms that may arise for a carbon atom described by the ground state configuration.

The electron configuration is: 1s² 2s² 2p². We have two closed subshells, 1s and 2s, which both give ¹S₀. We may therefore concentrate on the p-shell with two equivalent p-electrons and form a similar scheme as above. In this we include only states that allowed with respect to the Pauli principle.

np np		MS
		1	0	-1
ML	2		(1+ 1-)
	1	(1+ 0+)	(1+ 0-) (1- 0+)	(1- 0-)
	0	(1+ -1+)	(1+ -1-) (0+ 0-) (-1+ 1-)	(1- -1-)
	-1	(-1+ 0+)	(-1+ 0-) (-1- 0+)	(-1- 0-)
	-2		(-1+ -1-)

Now, the question is which terms hide among these states? We may use the following method:

1. Choose the state with highest M_S, in this case 1. This will also be the value of S for the term. Hence, the multiplicity defined by 2S+1 is 3.

2. Determine the highest M_L for this M_s. The value will also be the value of L for the term.

3. Cross out one state function in each cell which correspond to the possible quantum numbers M_L = -L, -L+1,..,0,..L-1,L and M_S = -S, -S+1,..,0,..S-1,S

4. Repeat the procedure stepwise for remaining functions.

We apply this to the wavefunctions given in the table.

1. Max M_S=1 S = 1 i.e. a triplet.

2. Max M_L=1 L = 1 i.e. a P-state.

The term is thus ³P.

3. Cross out a state function in each cell within the 3*3-matrix that is defined by

M_L=-1,0,1 and M_S=-1,0,1

4. Now there remain state functions only in the central column, i.e. for M_S=0 which means that only singlet states remain. We choose max M_L=2, i.e. a D-state.

The term is therefore ¹D.

5. We cross out a state function in each row, i.e. for M_L=-2, -1, 0, 1, 2

6. Only one state function remains corresponding to M_L=0 and M_S=0. The term is clearly ¹S.

In summary, we have obtained the following terms: ³P, ¹D, ¹S.

Accounting for the degeneracy, the total number of states that can be calculated for these terms is 9+5+1=15. This agrees also with the number of state functions in the table. Check that yourself.

In two examples we have shown the terms that may arise out of configurations with unfilled subshells. These terms have different energy and the question is what the energy order would be. In order to answer this question we shall use Hund's rules. They are as follows:

1. The ground state has highest possible S
2. It has highest possible L consistent with this S
3. It has highest possible J for more than half filled shell and smallest possible J for less than half filled shell.
4. In general, the rest of the terms can be arranged after the same principles.

Hund's rules can be applied to order the terms for a p²-configuration in sequence of energy.

We know that the terms which come into consideration are ³P, ¹D and ¹S. Hund's rules give directly the term that corresponds to the ground state: ³P

If we add the J quantum number representing the total angular momentum, we shall choose 0 since the shell is less than half filled (J can take the values 0, 1, 2, see part 2).

Next state is ¹D and the uppermost (with highest energy) is ¹S. We may now draw the following qualitative energy level diagram. A free carbon atom is normally in its lowest state, i.e. ³P

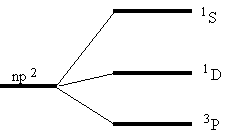
The energies of the energy levels can be obtained from handbooks in atomic physics. the following energies for the carbon atom: E(³P) = 0 eV; E(¹D) = 1,264 eV; E(¹S) = 2,684 eV;