JJ-coupling.

As we have seen above, the spin-orbit coupling depends very strongly upon the nuclear charge and for very heavy atom it may outweigh the electrostatic interaction Hes. In the perturbation approach, it is then necessary to first consider the influence from Hs-o and then, as an additional perturbation, consider Hes. Thus, in the first order perturbation, a number of independent electrons will be separately affected by the spin-orbit coupling. It is then appropriate to start with simultaneous eigenfunctions to H0, j and jz and we shall write these functions

For a two-electron system, the first order contribution to the energy then reads

As usual, the energy does not depend on mi, so the number of energy levels is determined by ji , i.e. from the angular momentum j = l + s of the individual electrons. For an np np'-configuration, j may take either of the values 3/2 or 1/2. For each np-electron this results in totally 6 states if we sum all mj levels. For the configuration we get totally 36 states in agreement with the LS-coupling case above. For equivalent electrons the number of states will be much more limited of course. We shall go through this as an example below.

When Hes is introduced as a small perturbation, the angular momenta are coupled together to give a total angular momentum J with the component Jz. Proper simultaneous wavefunctions may then be formulated in analogy with our earlier treatment of spin-orbit coupling as

where M is the eigenvalue of Jz. For our two-electron system this results in the following first order influence on the energy

EEs does not depend upon M.

The spin-orbit splitting of a-coupled p2-configuration. This is treated by using the spin-orbit coupling operator

and calculate the energy in the j1m1j2m2-representation, i.e. using the expression above. With l=1 and s=1/2 three sets of j-quantum numbers can be obtained as

The first gives the following contribution to the energy

This may be expanded to give

which may be calculated in the same way as before using the relationship

The result is

In the same way we get

and

In the next step we study the splitting of the spin-orbit split states. For this, we need to know which J:s are feasible for the different sets of j-quantum numbers. To be more precise, we go on considering two equivalent p-electrons. Special attention has to be paid to the Pauli principle and we therefore make some tables.

1. j1 = 3/2, j2 = 3/2

Since j1 and j2 are equal, m1 and m2 must be different. Note that the quantum numbers define the states, the electrons themselves are inseparable.

Now we may identify the states in the same way as we did for the LS-coupling case.

Max M = 2 J = 2 (M = 2, 1, 0, -1, -2)

Max M = 0 J = 0 (M = 0)

The total number of states is 2*2+1 + 2*0+1 = 6

2. j1 = 3/2, j2 = 1/2

Since in this case j1 j2 all combinations of m1 and m2 appear.

The states are identified as above.

Max M = 2 J = 2 (M = 2, 1, 0, -1, -2)

Max M = 1 J = 1 (M = 1, 0,-1)

The total number of states is in this case 2*2+1 + 2*1+1 = 8

3. j1 = 1/2, j2 = 1/2

Since j1 = j2 are again equal, m1 and m2 must be different. There is only one possible combination

Apparently, the state has J = 0.

The total number of states within the p2-configuration is thus 15, which agrees with the result we obtained for LS-coupling.

These three tables can be summarised in a more elegant way in one single table that reminds of the one we used in the LS-coupling case. This is what it looks like:

We may finally summarise all results in one diagram, including the states we got in the LS-coupling case. No attempt is made here to calculate the splitting caused by Hes but we treat it qualitatively as for the LS-coupling above. The interaction in the region where neither LS-coupling nor jj-coupling dominates is described by so-called intermediate coupling.

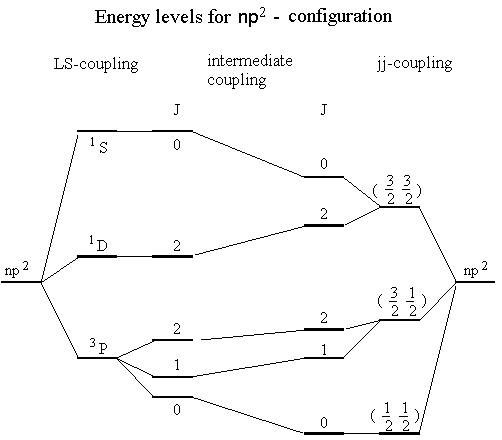
The LS-coupled and the jj-coupled sides of the diagram have been connected with lines going between energy levels associated with the same J, which obviously is a good quantum number whatever representation we use. The lines are drawn in a way that no crossing occurs between lines with the same J. They are drawn with due respect to the so-called "non-crossing rule".

The LS coupled energy levels may as we have seen above correspond to for example a carbon atom. If we compare atoms in the same group in the perodic table, the jj coupled case may then correspond to the Pb atom.


Last change: 21 February 2001