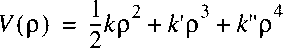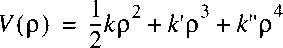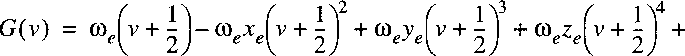Anharmonicity in the vibrational motion

The anharmonic vibrator can be represented with a potential function:
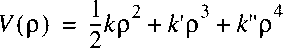On the basis of energies and wave functions of the harmonic oscillator, that can be used as a first approximation, quantum mechanical perturbation theory can be applied to find energy levels for the anharmonic oscillator (with parameters k` and k``):
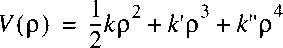In the usual spectroscopic practice an expansion is written (in cm^-1):
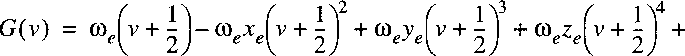with w_e, wexe, weye and weze to be considered as spectroscopic constants, that can be determined from experiment.
Note that for the anharmonic oscillator the separation between vibrational levels is no longer constant.
The solutions to the wave functions for an anharmonic oscillator are also different.

---

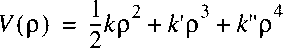
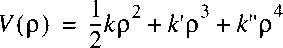
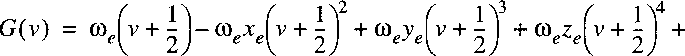
Last change: 18 February 2001