



Next: Centrale vierkante sferische potentiaal
Up: Schrödingervergelijking in drie dimensies
Previous: Oplossingen van de hoekvergelijkingen
Contents
Het radiële deel van de oplossing van de Schrödingervergelijking
voldoet aan
![\begin{displaymath}
{{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} \chi \over {...
...\over \hbar^2} \left[ V(r) - E \right] \chi =
l(l+1) \chi .
\end{displaymath}](img1345.png) |
(447) |
We gieten deze vergelijking in een andere vorm en beginnen met
een verandering van variabelen,
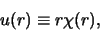 |
(448) |
waarmee 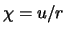 ,
,
![$d\chi /dr = [r(du / dr) -u]/r^2$](img1348.png) ,
,
![$(d/dr)[r^2(dR/dr)]=rd^2u/dr^2$](img1349.png) en dus
en dus
![\begin{displaymath}
-{\hbar^2 \over 2m}{d^2u\over dr^2}+ \left[ V + {\hbar^2 \over 2m}
{l(l+1) \over r^2} \right] u = Eu .
\end{displaymath}](img1350.png) |
(449) |
Dit wordt de radiële vergelijking genoemd en deze is
identiek in vorm aan de één-dimensionale Schrödingervergelijking,
behalve dat de effectieve potentiaal,
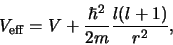 |
(450) |
een extra term bevat, de zogenaamde centrifugale term,
![$(\hbar^2 / 2m)[l(l+1)/r^2]$](img1352.png) . De term probeert het deeltje naar
buiten te drukken (weg van de oorsprong), net als een centrifugale
kracht in de klassieke fysica.
. De term probeert het deeltje naar
buiten te drukken (weg van de oorsprong), net als een centrifugale
kracht in de klassieke fysica.
De enige eis die we verder nog op kunnen leggen is die van
normering. Er dient te gelden dat
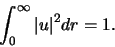 |
(451) |
Na het scheiden van de variabelen vinden we voor de golffunctie
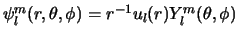 , , |
| |
waarbij  de oplossing is van de radiële vergelijking
met
de oplossing is van de radiële vergelijking
met 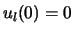 . Verder dient de functie
. Verder dient de functie  begrensd te zijn.
Meer kunnen we op dit punt niet zeggen. Daartoe hebben we
een precieze vorm van de potentiaal nodig.
begrensd te zijn.
Meer kunnen we op dit punt niet zeggen. Daartoe hebben we
een precieze vorm van de potentiaal nodig.




Next: Centrale vierkante sferische potentiaal
Up: Schrödingervergelijking in drie dimensies
Previous: Oplossingen van de hoekvergelijkingen
Contents
Jo van den Brand
2004-09-25
![\begin{displaymath}
{{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} \chi \over {...
...\over \hbar^2} \left[ V(r) - E \right] \chi =
l(l+1) \chi .
\end{displaymath}](img1345.png)
![\begin{displaymath}
{{\rm d} \over {\rm d} r} \left(
r^2 {{\rm d} \chi \over {...
...\over \hbar^2} \left[ V(r) - E \right] \chi =
l(l+1) \chi .
\end{displaymath}](img1345.png)
![\begin{displaymath}
-{\hbar^2 \over 2m}{d^2u\over dr^2}+ \left[ V + {\hbar^2 \over 2m}
{l(l+1) \over r^2} \right] u = Eu .
\end{displaymath}](img1350.png)