



Next: Oplossingen van de hoekvergelijkingen
Up: Schrödingervergelijking in drie dimensies
Previous: Schrödingervergelijking in drie dimensies
Contents
De tijdonafhankelijke Schrödingervergelijking in drie dimensies
luidt als volgt,
![\begin{displaymath}
{\bf H} \psi =
= - {\hbar^2 \over 2m} \left[ {1 \over r^2...
...r \partial \phi^2} \right] \psi ({\bf r})
= E\phi ({\bf r}).
\end{displaymath}](img1309.png) |
(425) |
We gaan nu deze vergelijking in sferische
coördinaten oplossen met behulp van de techniek van het scheiden
van variabelen. Hiertoe proberen we de oplossing
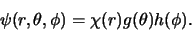 |
(426) |
We substitueren
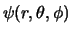 in de Schrödingervergelijking
in de Schrödingervergelijking
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {1 \over r^2}{\partial \over
\p...
... \partial \theta} \right) \right]
+ V(r) \chi gh = E \chi gh
\end{displaymath}](img1312.png) |
(427) |
en kunnen dit herschrijven als
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {gh \over r^2}{{\rm d} \over
{\...
...{\rm d} \theta} \right) \right]
+ V(r) \chi gh = E \chi gh .
\end{displaymath}](img1313.png) |
(428) |
We vermenigvuldigen de vergelijking met
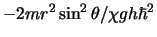 en krijgen
en krijgen
![\begin{displaymath}
{1 \over h}{{\rm d}^2 h \over {\rm d} \phi^2} =
{-\sin^2{\...
...m \over \hbar^2}r^2 \sin^2{\theta}
\left[ E - V(r) \right] .
\end{displaymath}](img1315.png) |
(429) |
De linkerkant van bovenstaande vergelijking hangt niet af van 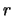 of
of
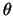 , terwijl de rechterzijde niet afhangt van
, terwijl de rechterzijde niet afhangt van 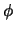 . De uitdrukkingen
aan beide kanten van het gelijkteken dienen derhalve gelijk te zijn
aan een constante. Hiervoor kiezen we
. De uitdrukkingen
aan beide kanten van het gelijkteken dienen derhalve gelijk te zijn
aan een constante. Hiervoor kiezen we 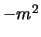 en verkrijgen
de volgende twee differentiaalvergelijkingen.
en verkrijgen
de volgende twee differentiaalvergelijkingen.
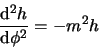 |
(430) |
en
![\begin{displaymath}
-{1 \over \chi} {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm...
...}r^2 \left[ E - V(r) \right]
= -{m^2 \over \sin^2{\theta}}.
\end{displaymath}](img1318.png) |
(431) |




Next: Oplossingen van de hoekvergelijkingen
Up: Schrödingervergelijking in drie dimensies
Previous: Schrödingervergelijking in drie dimensies
Contents
Jo van den Brand
2004-09-25
![\begin{displaymath}
{\bf H} \psi =
= - {\hbar^2 \over 2m} \left[ {1 \over r^2...
...r \partial \phi^2} \right] \psi ({\bf r})
= E\phi ({\bf r}).
\end{displaymath}](img1309.png)
![\begin{displaymath}
{\bf H} \psi =
= - {\hbar^2 \over 2m} \left[ {1 \over r^2...
...r \partial \phi^2} \right] \psi ({\bf r})
= E\phi ({\bf r}).
\end{displaymath}](img1309.png)
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {1 \over r^2}{\partial \over
\p...
... \partial \theta} \right) \right]
+ V(r) \chi gh = E \chi gh
\end{displaymath}](img1312.png)
![\begin{displaymath}
-{\hbar^2 \over 2m} \left[ {gh \over r^2}{{\rm d} \over
{\...
...{\rm d} \theta} \right) \right]
+ V(r) \chi gh = E \chi gh .
\end{displaymath}](img1313.png)
![\begin{displaymath}
{1 \over h}{{\rm d}^2 h \over {\rm d} \phi^2} =
{-\sin^2{\...
...m \over \hbar^2}r^2 \sin^2{\theta}
\left[ E - V(r) \right] .
\end{displaymath}](img1315.png)
![\begin{displaymath}
-{1 \over \chi} {{\rm d} \over {\rm d} r} \left(
r^2 {{\rm...
...}r^2 \left[ E - V(r) \right]
= -{m^2 \over \sin^2{\theta}}.
\end{displaymath}](img1318.png)