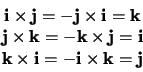Next: Determinantnotatie voor het uitwendig
Up: Vectorrekening over de reële
Previous: Inwendig of scalair product
Contents
Definitie:
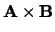 is een vector
is een vector 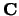 waarvan
waarvan
- de absolute waarde gelijk is aan
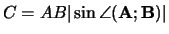 en
en
- (als
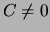 ) de richting bepaald worden door
) de richting bepaald worden door
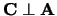 en
en
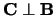 , terwijl de richting van voortgang van
, terwijl de richting van voortgang van 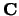 volgens
de rechterhandregel past bij de richting van draaiing van
volgens
de rechterhandregel past bij de richting van draaiing van 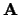 naar
naar 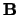 over
de kleinste hoek.
over
de kleinste hoek.
Merk op dat de grootte van het uitwendig product
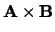 gelijk is
aan de oppervlakte van de op
gelijk is
aan de oppervlakte van de op 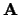 en
en 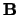 als zijden beschreven
parallellogram.
als zijden beschreven
parallellogram.
Voor het uitwendig product gelden de eigenschappen
-
![$\forall_{{\bf A},{\bf B}} [ {\bf B} \times {\bf A} = - ({\bf A} \times {\bf B}) ]$](img135.png) anti-commutativiteits eigenschap.
anti-commutativiteits eigenschap.
-
![$\forall_{{\bf A},{\bf B},{\bf C}} [ {\bf A} \times ({\bf B} + {\bf C})
= {\bf A} \times {\bf B} + {\bf A} \times {\bf C} ]$](img136.png) distributiviteits eigenschap.
distributiviteits eigenschap.
Uit de definitie volgt
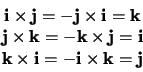 |
(5) |
en
 |
(6) |
In het bijzonder geldt dus dat
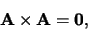 |
(7) |
en dus ook
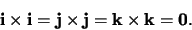 |
(8) |
Volgens de distributiviteits eigenschap is dus
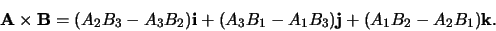 |
(9) |
Merk op dat als
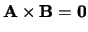 , dan
, dan 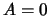 of
of 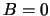 of
of
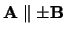 .
.




Next: Determinantnotatie voor het uitwendig
Up: Vectorrekening over de reële
Previous: Inwendig of scalair product
Contents
Jo van den Brand
2004-09-25