



Next: Som van matrices
Up: Matrixrekening
Previous: Product van een matrix
Contents
Als
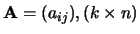 , dan definieert
, dan definieert
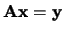 een afbeelding van
een afbeelding van 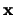 naar
naar
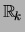 ,
,
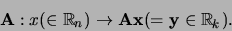 |
(232) |
Deze afbeelding is blijkbaar een lineaire afbeelding, want
-
![$\forall_{{\bf x},{\bf y} \in {\mathbb{R}}_n}
[{\bf A}({\bf x} + {\bf y}) = {\bf Ax} + {\bf Ay} ]$](img795.png) en
en
-
![$\forall_{{\bf x} \in {\mathbb{R}}_n, p \in {\mathbb{C}}}
[{\bf A}(p{\bf x}) = p {\bf Ax} ]$](img796.png) .
.
Stellingen:
- Als
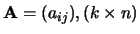 , terwijl
, terwijl
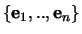 de basis van
de basis van
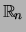 is,
dan is
is,
dan is 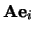 de
de  -kolomvector van
-kolomvector van
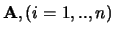 .
.
- Als
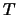 een lineaire afbeelding is van
een lineaire afbeelding is van
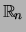 naar
naar
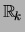 , dan bestaat er een matrix
, dan bestaat er een matrix
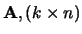 ,
zodanig , dat voor elke
,
zodanig , dat voor elke
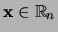 geldt, dat het
beeld van
geldt, dat het
beeld van 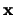 onder de transformatie
onder de transformatie 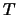 (dus
(dus 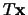 ) gelijk
is aan het product
) gelijk
is aan het product 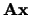 .
Deze matrix
.
Deze matrix 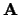 is de matrix waarvan de
is de matrix waarvan de  -kolomvector,
-kolomvector,
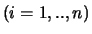 , het
, het 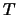 -beeld van de
-beeld van de  basisvector
basisvector 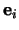 van
van
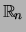 (dus
(dus 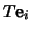 )
is. Deze
)
is. Deze 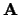 heet de transformatiematrix van de
afbeelding
heet de transformatiematrix van de
afbeelding 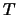 .
.
Jo van den Brand
2004-09-25