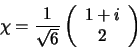Next: Consequenties van een meting
Up: Matrix representatie van spin
Previous: Spinoren
Contents
We gaan het matrixformalisme voor spin-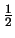 deeltjes nu
toepassen. Allereerst berekenen
we de verwachtingswaarde van
deeltjes nu
toepassen. Allereerst berekenen
we de verwachtingswaarde van 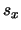 voor de spintoestand
voor de spintoestand 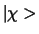 .
We vinden
.
We vinden
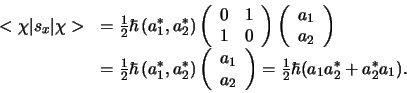 |
(584) |
Evenzo berekenen we
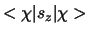 . Er geldt
. Er geldt
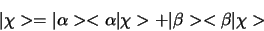 |
(585) |
en dus
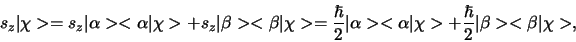 |
(586) |
waarmee we vinden
![\begin{displaymath}
< \chi \vert s_z \vert \chi >
= {\hbar \over 2} \left[ \v...
...ver 2} \left[ \vert a_1 \vert^2 - \vert a_2 \vert^2 \right] .
\end{displaymath}](img1641.png) |
(587) |
We zien dat respectievelijk
de eerste en tweede term de waarschijnlijkheid geven dat het
deeltje in de spintoestand 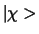 spin up of spin down heeft.
spin up of spin down heeft.
Voorbeeld: Stel voor dat een spin-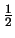 deeltje
zich in de toestand
deeltje
zich in de toestand
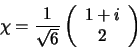 |
(588) |
bevindt. Als we 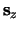 meten, dan is de waarschijnlijkheid
om
meten, dan is de waarschijnlijkheid
om 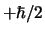 te vinden gelijk aan
te vinden gelijk aan
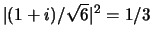 en de waarschijnlijkheid om
en de waarschijnlijkheid om 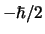 te vinden
te vinden
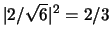 . Als we
. Als we 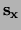 meten, dan is
de waarschijnlijkheid om
meten, dan is
de waarschijnlijkheid om 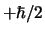 te meten
te meten
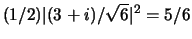 , terwijl de waarschijnlijkheid
om
, terwijl de waarschijnlijkheid
om 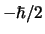 te vinden gelijk is aan
te vinden gelijk is aan
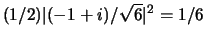 . Klaarblijkelijk is
de verwachtingswaarde van
. Klaarblijkelijk is
de verwachtingswaarde van 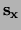 gelijk aan
gelijk aan
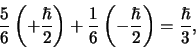 |
(589) |
hetgeen we ook meer rechttoe reachtaan hadden kunnen vinden,
 |
(590) |




Next: Consequenties van een meting
Up: Matrix representatie van spin
Previous: Spinoren
Contents
Jo van den Brand
2004-09-25
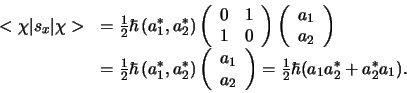
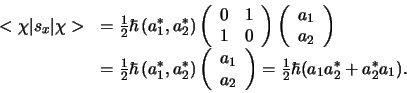
![]() deeltje
zich in de toestand
deeltje
zich in de toestand