4.2 THE POTENTIAL STEP

In this section, we examine the propagation of a wavepacket encountering a step change in potential located at the centre of the field of view, ie at position x = 0. The step types examined are:

"Small" Potential Step-Up

First recall the results for a plane harmonic wave striking a potential step: If an incident plane wave of wavevector ki, kinetic energy ki^2 (remembering that in our units m=1/2, h bar =1) were to strike the step from the left, then the conservation of energy would imply that on the right hand side of the step the transmitted wavevector kt would be related to the incident wavevector by,

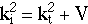
Eqtn 4.2.1

The usual analysis done in most standard quantum mechanics texts shows that the reflection coefficient for a plane wave is given by,

Eqtn 4.2.2

Although we do not work here with a simple plane wave, we expect these results to be a useful guide since as shown in Sec. 3 "The Initial Wavepacket", the spectral content of the wavepacket is a relatively narrow distribution of plane waves centred on k0 = 100 pi.
The following movie shows a wavepacket with k0 = 100 pi incident on a step of size equal to 0.64 (k0^2), where the fraction .64=16/25 has been chosen for numeric convenience in equation 4.2.1. In words, the step size is 64% of the mean incident kinetic energy:-

  1. QT Movie 4.2.2: "Small" Potential Step-Up - High-Resolution (760kbytes) .
The points to note are: The following exercises are suggested:-

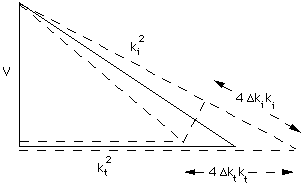
Fig 4.2.2. Energy and Wavevector Relationship for Step Potentials

Moderate Potential Step Up

The following movie shows the wavepacket incident on a step which is 80/81 times the mean incident energy. The ratio has been chosen so that the reflection coefficient for a plane wave of wavevector 100pi is 0.64 and the incident and transmitted wavevectors would be in the ratio of 9:1.
  • QT Movie 4.2.3: "Modest" Potential Step-Up (970kbytes)

    •  

     

    The points discussed above for the small step are also pertinent here; note in particular the much slower velocity of the transmitted wavepacket (recalling that the mean velocity is just 2k, and the transmitted wavevector is 9 times smaller than the incident one).

    Large Potential Step Up

    The movie below shows the wavepacket incident on a potential up-step equal in magnitude to 150% of the mean incident kinetic energy. Points to note are the total reflection, and the substantial interference between incoming and outgoing wavepackets. This should be compared with the gradual step shown later.
     
  • QT Movie 4.2.4: "Large" Potential Step-Up (434kbytes)

    • Rounded Potential Step Up

    This movie shows the effect of rounding the abrupt step. The potential rises from zero as one side of a gaussian function with width of 0.05 distance units, to a final value at x = 0 of 150% of the mean incident kinetic energy. The interference between incoming and outgoing waves is greatly reduced, and further broadening of the transition eliminates the interference patterns.
     
  • QT Movie 4.2.5: Rounded Potential Step-Up (918kbytes)

    • Step Down

    This movie shows the wavepacket incident on a potential step down of magnitude equal to -0.5625 = -9/16 of the mean incident kinetic energy. (The ratio has been chosen so that the reflection coefficient calculation is simple). Points to note are the increased velocity on the right hand side of the barrier, consequent on a greater mean wavevector, and the abrupt increase in width and decrease in amplitude on crossing the step. The fractional change in width can again be calculated from the pythagorean relation shown in Fig 4.2.2.
     
  • QT Movie 4.2.6: Potential Step-Down (510kbytes)

    •  

     

    The velocity can be checked against the prediction of 2ktransmit as an exercise. The reflection coefficient is quite small, and so we show in the following graph the last frame of the movie on an expanded scale:
     
     

    Fig 4.2.3. Wavepacket Reflected at a Potential Step-Down

    Ramped Potential Step Up

    It is interesting to compare the cases of a simple potential step with an equivalent linear ramp which rises from zero to the same value as the step. We choose a final value which is 0.64 k0^2, which is the same as the "small step-up" shown earlier, and a ramp rising from zero to the final value over a length of .05 distance units:
     
  • QT Movie 4.2.7: Ramped Potential Step-Up (510kbytes)

    •  

     

    The pertinent features are first, that the interference patterns are again minimal for a more gradual change in potential than an abrupt step, but more interesting is that the classical relation

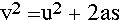
    Eqtn 4.2.3

    emerges from a consideration of the wavepacket motion. In the ramp region, the classical force on the particle would be -dV/dx, effective over a distance equal to the ramp length s (=0.05 here), and the acceleration for a mass 1/2 would therefore be,

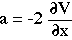
    Eqtn 4.2.4

    Now the mean wavepacket wavevectors on either side of the step are related through the energy conservation relation Eq 4.2.1 which may be reformulated as follows:

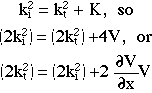
    Eqtn 4.2.5

    But the mean wavepacket velocity is just 2ki, 2kt on the two sides of the barrier, and so we find that the wavepacket follows the classical kinematic relation.Exercise: The particle velocities can be measured directly from the graph and related through the force on the particle to test the classical kinematic relation Eq 4.2.3.
     

    The Anti-Reflection Coating

    In elementary classical optics, students learn how an anti-reflection coating can be applied to the surface of lenses. The conditions for cancellation are that the reflected waves from the first and second interface are equal in amplitude but opposite in phase: this requires that the two interfaces are are one-quarter wavelength apart and that the refractive index of the coating is equal to the geometric mean of the indices for the two surrounding media, so that the reflection amplitudes are equal. Then the total path difference is one half wavelength, with identical phase shifts on reflection, and equal amplitudes, and so destructive interference occurs. The same principle applies here; by introducing a thin layer in which the wavevector k in the coating is equal to the geometric mean of the incident and transmitted wavevectors the reflection coefficient vanishes:-

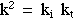
    Eqtn 4.2.6

    This again corresponds to a cancellation between the two reflected waves when the interfaces are one quarter wavelength apart;In the case of a wavepacket which contains a distribution of wavevectors, the anti-reflection property can only correspond to minimal rather than absolute lack of reflection, but nonetheless the effect is quite clear as is shown in the following movie. We show the standard wavepacket incident on a "small" potential step of height equal to 64% of the mean incident kinetic energy:-
     
  • QT Movie 4.2.8: Anti-Reflection Potential Profile (513kbytes)

    •  

     

    For comparison, you may want to have another look at the same size step without the anti-reflection coating:-

  • QT Movie 4.2.2 "Small" Potential Step-Up (760kbytes)

    •  

     

    Exercise: By matching the wavefunctions and their derivatives at the two boundaries in the usual manner (eg see Merzbacher), prove Eqtn 4.2.6.

    Comments, etc to: jo@nat.vu.nl