4.5 THE PERIODIC POTENTIAL
The periodic potential is a particularly important example because of its
application to crystalline solids. The basic result, as discussed in various
books on solid state physics (eg. Kittel),
is that the energy versus wavevector relation is modified from the parabolic
form for a free particle whenever the wavevector is close to integral multiples
of pi/a, where a is the period of the potential. At each of these wavevector
values a gap opens up in the energy vs. wave vector relation, and there
are no propagating wave solutions for the Schroedinger equation for energies
which lie within the gaps. The result is shown below:
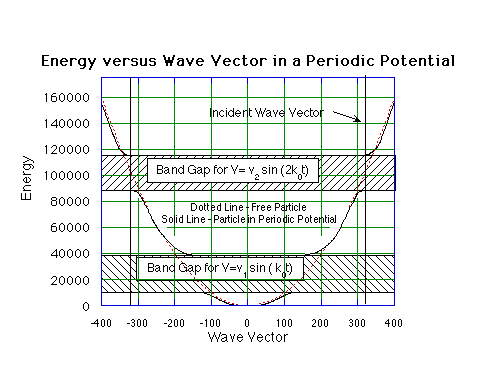
Fig 4.5.1. Energy versus wave vector in a periodic potential.
The magnitude of the gap is directly related to the amplitude of the
fourier component of the potential at the corresponding frequency. If the
potential is written as,
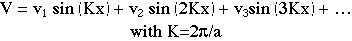
Eqtn 4.5.1
then the band gaps are,

Eqtn 4.5.2
Here we work with a single spatial frequency component K for
the potential energy, and first investigate what happens when K=k0,
the mean wavevector of the incident wavepacket. This should put the wavepacket
well above the bandgap region which is located at k = K/2 (see Fig
4.5.1). The band gap V1 is fixed at 30% of
the mean incident kinetic energy k0^2. The
following movie shows that the wavepacket is indeed little affected by
the sinusoidal potential energy. (We denote in the movie the region occupied
by the crystal/periodic potential by a rectangular box which starts at
x = -0.1 and extends to x = +0.3, since the actual potential
itself oscillates too fast to be effectively displayed with the available
resolution on the screen)
There is some reflection from the abrupt potential discontinuity at the
start of the "crystal", but the transmitted wave packet propagates freely
through the periodic potential, albeit with some superposed oscillations.
At the end of the movie, the wavepacket is just starting to emerge from
the crystal, and it is interesting to see that these oscillations disappear.
If we now choose the lattice wave vector K equal to 2k0,
the mean energy of the incident wave packet lies exactly at the centre
of the resulting band-gap (see Fig 4.5.1):
The incident wave packet is essentially completely reflected, as it cannot
propagate through the crystal.
It is interesting to consider what happens when the mean incident energy
lies close to a band gap but not actually in it. The free-particle parabolic
energy-wavevector relationships are distorted there and approach the band-gap
edge asymptotically. The group velocity goes to zero at the band edge and
the solutions of Schroedinger's equation are standing waves there. In the
following movie, we show the standard wave packet approaching a crystal
where the spatial wavevector K is 1.8k0.
The wavepacket centred at k0 is thus just above
the band gap located at k=0.9k0.
NEGATIVE EFFECTIVE MASS:
Finally, we look at the situation of an external force (a potential gradient)
applied to the packet in the presence of the periodic potential. This is
a very interesting case because when the incident wavevector is such that
the particle energy lies at the top of an allowed band, the "effective
mass" is negative. (It is shown in the standard texts on solid state physics
(eg. Kittel) that a particle close to a band
edge in a crystal should respond to an external force field as if it had
an effective mass given by the inverse of the second derivative of the
dispersion relation. Near the top of an allowed band, this is negative,
and so we expect a wave packet which would normally be accelerated by an
external force to be slowed by the force in the presence of the periodic
potential. In the following movies, we show what happens
-
With the crystal periodic potential only
-
With an external force only
-
With both an external force and the periodic potential
for the case where the spatial wavevector K is 2.5k0.The
band gap is located at k=1.25k0, and so the
incident wavepacket lies just below it, and should propagate freely through
the crystal as shown below:
(An extended time was chosen for this movie for purposes of later clarity
in Movie 4.4.6, and so the the particle is seen to collide with what is
in effect a perfectly reflecting wall at at x = .5. This "wall"
arises from the boundary condition psi(x = ±0.5) = 0 implicit
in the process used to solve the Schroedinger equation.) Now we remove
the periodic potential, and add a ramp potential decreasing towards the
right from V=0 at x=0 to V=-k0^2
at
x=-.5. This corresponds to a constant force acting towards the right,
which should accelerate the particle to the right as shown below.
(Again the longer time sequence, and the force, mean that the particle
collides with the effective wall at x = -.5)
Finally, we show the effect of having both the periodic potential and
the right-directed force:-
The particle is slowed and its direction of travel reversed in the
presence of a force which would normally accelerate it. Of course, the
point here is that the particle is not subject to the external force alone,
but to the combination of the external force and the force arising
from the periodic potential, so we should not base our expectations on
the external force alone anyway.
Reference: "Introduction to Solid State Physics",
C. Kittel, John Wiley & Sons Inc., New York, 1986, 6th edition.
Comments etc to :
jo@nat.vu.nl