4.4 Single and Multiple Potential Wells
The Single Well
A potential well can be formed in many ways. Here, we restrict ourselves
to a well which is bounded by two rectangular potential barriers, separating
it from surrounding regions where the potential is the same as within the
well. Transmission of a plane wave through such a well is a soluble problem,
(eg see Merzbacher) and gives some insight into what to expect for a wavepacket.
Hence we first show a movie, not of a wavepacket, but one which displays
the transmission tunnelling probability for a plane wave. The wavepacket
is of wavevector k and approaches barriers of variable height but fixed
width (.005 distance units); the well width is fixed at .0045 units.:-
The resonances where the transmission probability rises to unity are clearly
evident. These resonances correspond to the energy of the incident wave
coinciding with the energy of the metastable states formed in the well
when the waves undergoing successive partially reflected from the internal
walls are in phase with each other.The effect of varying the well width
is also of interest:-
Here we see that as the well becomes wider, the resonances move to lower
wavevectors as expected, since to first order each resonance corresponds
to a half-integral numbers of wavelengths between the walls: roughly, the
resonances occur for well widths equal to 2*pi*(2n+1)/k. (Note that
the limited horizontal resolution used here, prescribed by Excel, and the
narrow width of the resonances, means that the curves do not always rise
fully to unity in Movie 4.4.2 when the resonance width is less than the
horizontal resolution on the movie of 1 part in 250).With this background,
it is interesting to examine the scattering of a wavepacket from such a
well when the mean incident wavevector corresponds both to an off-resonance
condition, and to a resonance condition. Both of the following movies show
the standard wavepacket approaching a well whose barriers are 237,000 energy
units high and .005 distance units wide, but for Movie 4.4.3 the well is
.0035 units wide, whilst for Movie 4.4.4 the well is .0045 units wide:-
In the non-resonant case, the incident wavepacket is substantially reflected,
and there is only a very weak transmission. However, in the resonant case,
several features of interest can be seen. First there is a strong reflection
from the basic potential discontinuity, followed by a second, weaker reflection.
There is a substantial transmission. Most dramatically, there is a clear
and strong intra-well resonance, corresponding to the excitation of the
meta-stable state. This state then decays, giving rise to the transmitted
wavepacket and the weaker, second component of the reflected wavepacket,
which therefore thus takes on an overall double-pulse shape. Resonant wavepacket
tunnelling of this type has been analysed by A. Edgar,
Am. J. Phys,
63, 136-141, 1995, and the shape of the reflected wavepacket explained.
Resonant tunnelling barrier structures have been fabricated using Molecular
Beam Epitaxy techniques, resonant tunnelling observed, and devices using
resonant tunnelling made, and so this topic has practical as well as theoretical
interest.
The Double Well
Putting three identical barriers together gives rise to the double well
structure. Again, we confine ourselves to rectangular barriers since it
is useful to look at the analytical results for plane waves first. In the
following two movies we show the transmission tunnelling probability for
plane
waves as a function of barrier height and well width. The two wells
are of identical geometry:
(Here the well width is fixed at .0045 units, and the barrier width at
.005 units)
(Here the barrier height is fixed at 237,000 energy units, and the barrier
width at .005 distance units).
The key points to note in both movies are the double resonances which
now occur, corresponding to the symmetric and antisymmetric metastable
states which to first order correspond to :-
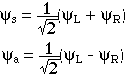
Eqtn 4.4.1
Here the two functions psi left and psi right are the wavefunctions
describing the metastable states in the individual wells. The following
two movies show resonant tunnelling for the double well structure: the
standard wavepacket is incident on a double well with the mean incident
wavevector corresponding to the average of the two resonant wavevectors.
The standard wavepacket approaches a well whose barriers are 237,000 energy
units high and .005 distance units wide, whilst the well is .0045 units
wide:-
The in-well resonance can be seen in Movie 4.4.7, but is clearer if we
choose an expanded scale view showing just the central region:-
The oscillation of the probability amplitude between one well and the other
is now clear. This tunnelling oscillation is described in the standard
textbooks (eg Merzbacher) and underpins the theory
of the tunnelling splitting observed in the spectrum of the ammonia molecule.
The frequency corresponding to energy difference between the symmetric
and antisymetric states, in the units used here (m=1/2, h bar=1)
is just the difference,
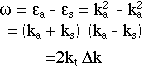
Eqtn 4.4.2
Here kr is the average of the two resonant wavevectors
and delta k is their difference. The frequency at which the particle shuttles
to and fro between the wells is just one-half of this frequency (Merzbacher):
Suggestion: Measure the tunnelling frequency from the movie and
compare it with the prediction, using k and delta k from
Movie 4.4.5
Four Wells
Finally , as a transition to the case of the infinite periodic potential,
we show the case of four potential wells which have a set of four closely
spaced tunnelling resonances where there were two for the double well case.
The standard wavepacket is incident on a set of identical barriers of height
237,000 energy units, width .005 distance units, and well width of .0045
distance units.
Periodic potentials are discussed in Section 4.5.
Reference: "Quantum Mechanics", E. Merzbacher,
Wiley International, New York, 1970, 2nd edition, p74
Comments etc to :jo@nat.vu.nl